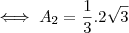Seja o triângulo ABC, onde A(0, 0), B(2, 0) e C(2, 2?3). Se a medida do ângulo interno referente ao vértice A for reduzida em 50%, a área do triângulo ficará
a) 75% menor b) 50% menor c) 33% menor d) 30% menor e) 25% meno
Bom, eu montei o triangulo, usei teorema de pitagoras para encontrar a hipotenusa e usei a relação cosseno para achar os valores dos angulos e ficou assim:

Bom reduzindo em 50% o ângulo A sei que ficará:

Mas não sei qual a relação disso com os lados -(.
Me ajude por favor.


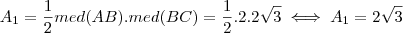 .
.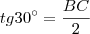 , mas
, mas 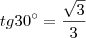 , então:
, então: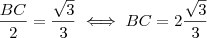 .
. .
.