 por MERLAYNE » Qua Abr 04, 2012 19:00
por MERLAYNE » Qua Abr 04, 2012 19:00
A EXPRESSÃO
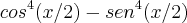
É IGUAL A:
PS: NÃO TENHO A MÍNIMA NOÇÃO DO QUE FAZER! AGRADEÇO A AJUDA DESDE JÁ!
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 04, 2012 19:23
por MarceloFantini » Qua Abr 04, 2012 19:23
Vou lembrar algumas relações trigonométricas importantes: primeiro, a relação fundamental
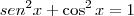
; segundo, o cosseno do arco duplo

; por último, a fatoração de diferença de potências à quarta
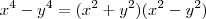
. Tente usar estes fatos para a resolução do exercício.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MERLAYNE » Qua Abr 04, 2012 19:34
por MERLAYNE » Qua Abr 04, 2012 19:34
MarceloFantini escreveu:Vou lembrar algumas relações trigonométricas importantes: primeiro, a relação fundamental
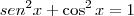
; segundo, o cosseno do arco duplo

; por último, a fatoração de diferença de potências à quarta
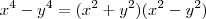
. Tente usar estes fatos para a resolução do exercício.
Obrigada, eu sei todas essas relações porém não estou conseguindo ultilizá-las e tenho a informação que

e

está correto ultlizar essa informação nessa equação?
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 04, 2012 19:41
por MarceloFantini » Qua Abr 04, 2012 19:41
Por favor, procure escrever tudo corretamente no LaTeX. O código é
- Código: Selecionar todos
\cos^2 \left( \frac{x}{2} \right) = \frac{1 + \cos x}{2}
que sai
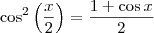
. Sim, elas são válidas, porém não levarão à resolução mais rápida do exercício. Além disso, elas são consequência das duas primeiras relações que escrevi.
Façamos isso passo a passo. Primeiro, escreva a fatoração das potências à quarta na expressão dada.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MERLAYNE » Qua Abr 04, 2012 20:14
por MERLAYNE » Qua Abr 04, 2012 20:14


MarceloFantini escreveu:Por favor, procure escrever tudo corretamente no LaTeX. O código é
- Código: Selecionar todos
\cos^2 \left( \frac{x}{2} \right) = \frac{1 + \cos x}{2}
que sai
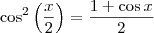
. Sim, elas são válidas, porém não levarão à resolução mais rápida do exercício. Além disso, elas são consequência das duas primeiras relações que escrevi.
Façamos isso passo a passo. Primeiro, escreva a fatoração das potências à quarta na expressão dada.
Então no caso fica
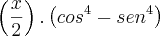
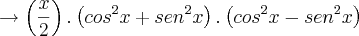
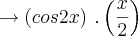
SÓ NÃO SEI MAIS DEPOIS DAI...
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 04, 2012 20:25
por MarceloFantini » Qua Abr 04, 2012 20:25
Não tenha pressa. Sua fatoração não está correta. O caminho certo é
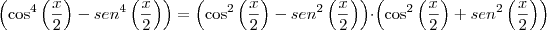
.
Agora, o que você pode dizer do fator direito e do fator esquerdo no produto?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MERLAYNE » Qua Abr 04, 2012 20:32
por MERLAYNE » Qua Abr 04, 2012 20:32
MarceloFantini escreveu:Não tenha pressa. Sua fatoração não está correta. O caminho certo é
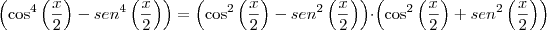
.
Agora, o que você pode dizer do fator direito e do fator esquerdo no produto?
O FATOR ESQUERDO É EQUIVALENTE A
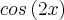
E O FATOR DIREITO É A RELAÇÃO FUNDAMENTAL EQUIVALENTE A

ESTÁ CORRETO?
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 04, 2012 20:46
por MarceloFantini » Qua Abr 04, 2012 20:46
O fator direito está certo, o esquerdo não. Não será
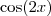
mas sim

. O arco é

e não apenas

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MERLAYNE » Qua Abr 04, 2012 21:05
por MERLAYNE » Qua Abr 04, 2012 21:05
MarceloFantini escreveu:O fator direito está certo, o esquerdo não. Não será
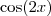
mas sim

. O arco é

e não apenas

.
entendi agora! muito obrigada
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Achar a equação da metade inferior da circunferência
por Caroline Oliveyra » Ter Jul 12, 2011 21:58
- 5 Respostas
- 5763 Exibições
- Última mensagem por Caroline Oliveyra

Qua Jul 13, 2011 15:44
Geometria Analítica
-
- arco
por cristina » Ter Set 22, 2009 15:03
- 2 Respostas
- 1561 Exibições
- Última mensagem por cristina

Ter Set 22, 2009 23:45
Trigonometria
-
- Arco de Circunferência
por gustavowelp » Dom Jun 27, 2010 11:42
- 3 Respostas
- 2352 Exibições
- Última mensagem por Douglasm

Dom Jun 27, 2010 12:33
Trigonometria
-
- comprimento do arco
por liviabgomes » Seg Mai 30, 2011 16:11
- 10 Respostas
- 6224 Exibições
- Última mensagem por liviabgomes

Qua Jun 01, 2011 15:03
Cálculo: Limites, Derivadas e Integrais
-
- arco duplo
por MERLAYNE » Qua Abr 04, 2012 19:52
- 1 Respostas
- 2501 Exibições
- Última mensagem por MarceloFantini

Qua Abr 04, 2012 23:57
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
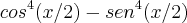 É IGUAL A:
É IGUAL A:
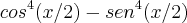 É IGUAL A:
É IGUAL A:
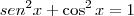 ; segundo, o cosseno do arco duplo
; segundo, o cosseno do arco duplo  ; por último, a fatoração de diferença de potências à quarta
; por último, a fatoração de diferença de potências à quarta 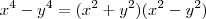 . Tente usar estes fatos para a resolução do exercício.
. Tente usar estes fatos para a resolução do exercício.

; segundo, o cosseno do arco duplo
; por último, a fatoração de diferença de potências à quarta
. Tente usar estes fatos para a resolução do exercício.
 e
e  está correto ultlizar essa informação nessa equação?
está correto ultlizar essa informação nessa equação?
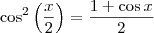 . Sim, elas são válidas, porém não levarão à resolução mais rápida do exercício. Além disso, elas são consequência das duas primeiras relações que escrevi.
. Sim, elas são válidas, porém não levarão à resolução mais rápida do exercício. Além disso, elas são consequência das duas primeiras relações que escrevi.



. Sim, elas são válidas, porém não levarão à resolução mais rápida do exercício. Além disso, elas são consequência das duas primeiras relações que escrevi.
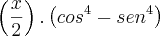
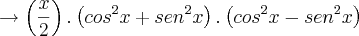
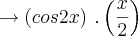

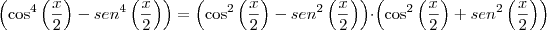 .
.

.
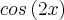 E O FATOR DIREITO É A RELAÇÃO FUNDAMENTAL EQUIVALENTE A
E O FATOR DIREITO É A RELAÇÃO FUNDAMENTAL EQUIVALENTE A  ESTÁ CORRETO?
ESTÁ CORRETO?
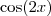 mas sim
mas sim  . O arco é
. O arco é  e não apenas
e não apenas  .
.

mas sim
. O arco é
e não apenas
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

