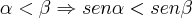por rola09 » Seg Mar 12, 2012 16:19
por rola09 » Seg Mar 12, 2012 16:19
Boa tarde a todos,
Gostaria que alguém me pudesse confirmar o resultado do seguinte exercício pois estou com algumas dúvidas no resultado.
"Quantas voltas dá a roda de uma bicicleta com 72 cm de diâmetro quando percorre 9 km."
Das 4 opções, duas são as seguintes:
- Aproximadamente 3979
- Aproximadamente 3981
Ora se 72 cm x pi = 226,194 > e 9000/2,2619 = 3978
Isto deve ter tudo a ver com arredondamentos, mas gostaria que alguém com mais experiência me confirmasse.
Obrigado
-
rola09
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Mar 12, 2012 15:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cientifico-Natural
- Andamento: cursando
 por LuizAquino » Seg Mar 12, 2012 17:33
por LuizAquino » Seg Mar 12, 2012 17:33
rola09 escreveu:Gostaria que alguém me pudesse confirmar o resultado do seguinte exercício pois estou com algumas dúvidas no resultado.
"Quantas voltas dá a roda de uma bicicleta com 72 cm de diâmetro quando percorre 9 km."
Das 4 opções, duas são as seguintes:
- Aproximadamente 3979
- Aproximadamente 3981
Ora se 72 cm x pi = 226,194 > e 9000/2,2619 = 3978
Isto deve ter tudo a ver com arredondamentos, mas gostaria que alguém com mais experiência me confirmasse.
Sabemos que o comprimento de uma circunferência de raio
r é dado por:

Como o diâmetro é 72 cm, temos que:
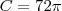
Usando a aproximação

, temos que:
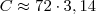
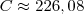
Sabemos que 9 km corresponde a 900.000 cm. Desse modo, o número
n de voltas é aproximadamente:
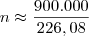
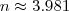
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rola09 » Seg Mar 12, 2012 18:34
por rola09 » Seg Mar 12, 2012 18:34
Sr. LuizAquino,
Desde já agradeço imenso a sua ajuda e resposta.
O raciocínio para mim também está correcto, mas pergunto se supostamente não deveríamos usar o valor de Pi sem arredondar, e se for o caso o resultado já vai dar 3979.
Sei que o resultado pouco interessa, desde que o raciocínio esteja correcto, mas neste caso e tratando-se de uma situação com escolha de apenas uma das opções, gostava de ter a resposta correcta e não tenho soluções do exercício para confirmar.
-
rola09
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Mar 12, 2012 15:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cientifico-Natural
- Andamento: cursando
 por LuizAquino » Seg Mar 12, 2012 19:10
por LuizAquino » Seg Mar 12, 2012 19:10
LuizAquino escreveu:Desde já agradeço imenso a sua ajuda e resposta.
O raciocínio para mim também está correcto, mas pergunto se supostamente não deveríamos usar o valor de Pi sem arredondar, e se for o caso o resultado já vai dar 3979.
Sei que o resultado pouco interessa, desde que o raciocínio esteja correcto, mas neste caso e tratando-se de uma situação com escolha de apenas uma das opções, gostava de ter a resposta correcta e não tenho soluções do exercício para confirmar.
Por convenção, em exercícios desse tipo usamos a aproximação:

.
Mas se for usada outra aproximação para

, então o resultado será diferente.
De qualquer modo, alguma aproximação será usada.
Sem usar qualquer aproximação, a reposta correta seria um número irracional:
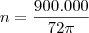
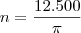
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rola09 » Dom Mar 18, 2012 17:59
por rola09 » Dom Mar 18, 2012 17:59
Quero aproveitar o tópico para colocar mais umas questões de escolha múltipla. Em que a minha resposta se encontra a
BOLT1 - Os planos
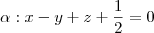
e
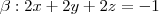
são:
(A) coicidentes
(B) perpendiculares
(c) secantes não perpendiculares(d) estritamente paralelos
2 - Uma equação vetorial da reta que passa em P (-1,2,3) e é perpendicular ao plano
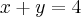
é:
(A)

(B)
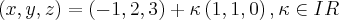 (C)
(C) 
(D)

3 - Considere, em

, a equação trignométrica
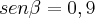
. Em qual destes intervalos esta equação tem uma única solução.
(A)
![\left[-\frac{\pi}{2};\frac{\pi}{2} \right] \left[-\frac{\pi}{2};\frac{\pi}{2} \right]](/latexrender/pictures/d46495c56430eb9a9254c21aa0d02ff2.png) (B)
(B) ![\left[0,\pi \right] \left[0,\pi \right]](/latexrender/pictures/401598234817b1f8eabc57f81da171d0.png)
(C)
![\left[\frac{\pi}{4};\frac{3\pi}{4} \right] \left[\frac{\pi}{4};\frac{3\pi}{4} \right]](/latexrender/pictures/6ed8d7cd7cd9a9d3bdfd5da6df309613.png)
(D)
![\left[-\frac{\pi}{4},\frac{\pi}{4} \right] \left[-\frac{\pi}{4},\frac{\pi}{4} \right]](/latexrender/pictures/d436e25f7064adbcb704f51a48c401b4.png)
4 - Dadas as proposições:
I. Existe um ângulo no IV quadrante cujo co-seno é 2.
II. Sendo

e

dois ângulos do III quadrante tem-se que:
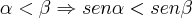
(A) I é verdadeira e II é falsa
(B) São ambas verdadeiras(C) São ambas falsas
(D) II é verdadeira e a I é falsa
5 - Na Figura, está representado o círculo trigonométrico.
Sabe-se que:
•? a recta r é tangente à circunferência no ponto A(1,0)
•? a recta s passa na origem do referencial e intersecta a recta r no ponto P, cuja ordenada é -2
•? o ponto Q, situado no segundo quadrante, pertence à recta s
Seja

a amplitude, em radianos, do ângulo orientado, assinalado na figura, que tem por lado origem o semieixo positivo Ox e por lado
extremidade a semi-recta OP.
Qual é o valor de

, arredondado às centésimas?

(A) -1.10
(B) -1.11(C) 1.10
(D) -2
-
rola09
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Mar 12, 2012 15:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cientifico-Natural
- Andamento: cursando
 por LuizAquino » Dom Mar 18, 2012 19:25
por LuizAquino » Dom Mar 18, 2012 19:25
rola09 escreveu:Quero aproveitar o tópico para colocar mais umas questões de escolha múltipla. Em que a minha resposta se encontra a
BOLT1 - Os planos
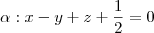
e
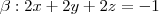
são:
(A) coicidentes
(B) perpendiculares
(c) secantes não perpendiculares(d) estritamente paralelos
2 - Uma equação vetorial da reta que passa em P (-1,2,3) e é perpendicular ao plano
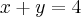
é:
(A)

(B)
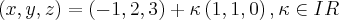 (C)
(C) 
(D)

3 - Considere, em

, a equação trignométrica
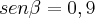
. Em qual destes intervalos esta equação tem uma única solução.
(A)
![\left[-\frac{\pi}{2};\frac{\pi}{2} \right] \left[-\frac{\pi}{2};\frac{\pi}{2} \right]](/latexrender/pictures/d46495c56430eb9a9254c21aa0d02ff2.png) (B)
(B) ![\left[0,\pi \right] \left[0,\pi \right]](/latexrender/pictures/401598234817b1f8eabc57f81da171d0.png)
(C)
![\left[\frac{\pi}{4};\frac{3\pi}{4} \right] \left[\frac{\pi}{4};\frac{3\pi}{4} \right]](/latexrender/pictures/6ed8d7cd7cd9a9d3bdfd5da6df309613.png)
(D)
![\left[-\frac{\pi}{4},\frac{\pi}{4} \right] \left[-\frac{\pi}{4},\frac{\pi}{4} \right]](/latexrender/pictures/d436e25f7064adbcb704f51a48c401b4.png)
4 - Dadas as proposições:
I. Existe um ângulo no IV quadrante cujo co-seno é 2.
II. Sendo

e

dois ângulos do III quadrante tem-se que:
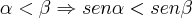
(A) I é verdadeira e II é falsa
(B) São ambas verdadeiras(C) São ambas falsas
(D) II é verdadeira e a I é falsa
5 - Na Figura, está representado o círculo trigonométrico.
Sabe-se que:
•? a recta r é tangente à circunferência no ponto A(1,0)
•? a recta s passa na origem do referencial e intersecta a recta r no ponto P, cuja ordenada é -2
•? o ponto Q, situado no segundo quadrante, pertence à recta s
Seja

a amplitude, em radianos, do ângulo orientado, assinalado na figura, que tem por lado origem o semieixo positivo Ox e por lado
extremidade a semi-recta OP.
Qual é o valor de

, arredondado às centésimas?

(A) -1.10
(B) -1.11(C) 1.10
(D) -2
Por favor, crie outros tópicos para cada uma de suas dúvidas.
Por questão de organização do fórum, cada tópico deve conter apenas uma questão.
Além disso, vale lembrar que não é objetivo desse fórum resolver listas inteiras de exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rola09 » Dom Mar 18, 2012 19:34
por rola09 » Dom Mar 18, 2012 19:34
Peço desculpa. Não era minha intenção criar confusão.
Pensei que pudesse aproveitar o tópico. Posso criar outro com este último post?
Queria apenas confirmar se os meus raciocínios estavam corretos visto que só tenho disponibilidade de estudar sozinho e quando descobri este fórum, já me tem ajudado bastante.
-
rola09
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Mar 12, 2012 15:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cientifico-Natural
- Andamento: cursando
 por LuizAquino » Dom Mar 18, 2012 19:41
por LuizAquino » Dom Mar 18, 2012 19:41
rola09 escreveu:Peço desculpa. Não era minha intenção criar confusão.
Ok.
rola09 escreveu:Pensei que pudesse aproveitar o tópico. Posso criar outro com este último post?
Como disse antes, nós recomendamos sempre que em cada tópico haja apenas um exercício. Em sua última mensagem há 5 exercícios!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



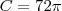
 , temos que:
, temos que: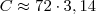
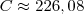
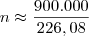
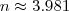

 , então o resultado será diferente.
, então o resultado será diferente.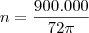
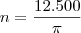
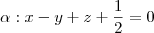 e
e 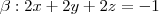 são:
são: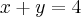 é:
é:
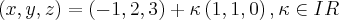


 , a equação trignométrica
, a equação trignométrica 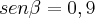 . Em qual destes intervalos esta equação tem uma única solução.
. Em qual destes intervalos esta equação tem uma única solução.![\left[-\frac{\pi}{2};\frac{\pi}{2} \right] \left[-\frac{\pi}{2};\frac{\pi}{2} \right]](/latexrender/pictures/d46495c56430eb9a9254c21aa0d02ff2.png)
![\left[0,\pi \right] \left[0,\pi \right]](/latexrender/pictures/401598234817b1f8eabc57f81da171d0.png)
![\left[\frac{\pi}{4};\frac{3\pi}{4} \right] \left[\frac{\pi}{4};\frac{3\pi}{4} \right]](/latexrender/pictures/6ed8d7cd7cd9a9d3bdfd5da6df309613.png)
![\left[-\frac{\pi}{4},\frac{\pi}{4} \right] \left[-\frac{\pi}{4},\frac{\pi}{4} \right]](/latexrender/pictures/d436e25f7064adbcb704f51a48c401b4.png)
 e
e  dois ângulos do III quadrante tem-se que:
dois ângulos do III quadrante tem-se que: