Parece-me que sua duvida nao é nem de trigonometria, não é ? =P
se eu entendi bem voce quer resolver a equação
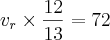
simplesmente ?
Explicando porcamente eu diria que voce deve "passar a fração para o outro lado, invertendo-a". e é maomeno isso mesmo. mas vou explicar melhor o por que:
temos isso :
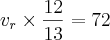
voce concorda que uma equação, assim como uma balança pode ser modificada IGUALMENTE dos dois lados sem que a igualdade seja violada ?
então vamos multiplicar ambos os lados da equação pela fração inversa à essa! por que ? simplesmente por que quando eu fizer

resultará em 1 e todo numero multiplicado a um é ele mesmo! observe :
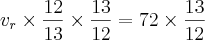
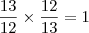
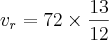
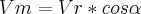
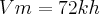
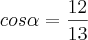
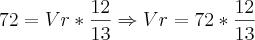


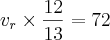 simplesmente ?
simplesmente ? resultará em 1 e todo numero multiplicado a um é ele mesmo! observe :
resultará em 1 e todo numero multiplicado a um é ele mesmo! observe :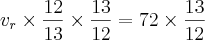
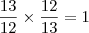
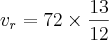

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)