[trigonometria]

por **Flavia R** » Qui Ago 25, 2011 12:07

Considerando-se que a equação $senx.cosx=\frac{\sqrt[2]{3}}{4}}$ tem n soluções no intervalo $[0,2\Pi]$ , pode-se afirmar que o valor de n é:

bom, eu tentei elevar os dois lados ao quadrado já, mas não fechou..

por **gvm** » Qui Ago 25, 2011 21:40

Bom, uma dica pra resolver esse tipo de exercício, onde você tem senx . cosx

em um dos membros é se lembrar das relações de Arco Duplo, mais especificamente dessa aqui:

sen (2x) = 2.senx.cosx

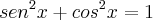Pensa em como utilizar isso no exercício em questão, você vai acabar chegando a uma expressão bem mais simples do que se elevasse os dois membros ao quadrado e utilizasse ${sen}^{2}x + {cos}^{2}x = 1$ para deixar toda a expressão em função do seno ou cosseno

Espero ter ajudado.

por **Flavia R** » Qui Ago 25, 2011 22:01

na verdade, eu não consigo ver como a fórmula do arco duplo pode me ajudar..:S

por **gvm** » Qui Ago 25, 2011 22:09

A expressão é a seguinte:

$senx . cosx = \sqrt[2]{3}/4$

Multiplicando os dois membros da equação por 2 obtem-se:

$2.senx . cosx = \sqrt[2]{3}/2$

Sabe-se que sen(2x) = 2.senx.cosx

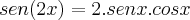, portanto:

$sen(2x) = \sqrt[2]{3}/2$

Agora que temos toda a expressão em função apenas do seno é só resolver normalmente e encontrar as soluções contidas no intervalo especificado, lembrando que as soluções da equação são os valores de

e não de

.

Esperto ter ajudado

[trigonometria]

[trigonometria]

[trigonometria]

Re: [trigonometria]

Re: [trigonometria]

Re: [trigonometria]

Quem está online