estou com dúvidas em duas questões: 1. Se sec
=![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e
, então 
é igual a:já tentei passar para sen e cos, para depois voltar à sec, mas não deu certo:
=
È por aí?
2. O gráfico da função definida por f(x)=x2 + bx + c
R, em que c=cos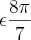
a) intercepta o eixo das abscissas em exatamente 2 pontos positivos
b) intercepta o eixo das abscissas em exatamente 2 pontos negativos
c) intercepta o eixo das abscisas em 2 pontos de sinais diferentes
d) intercepta o eixo das abscissas na origem
e) não intercepta o eixo das abscissas.
Essa não sei nem por onde começo.
?
).
.
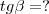
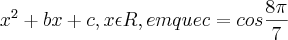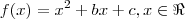, em que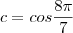 
. Escreva-o e pense como será o sinal dele.
é do 3º quadrante! E que um número ao quadrado é sempre positivo.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.