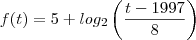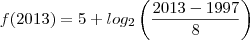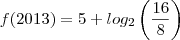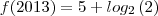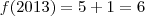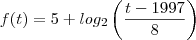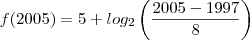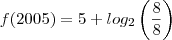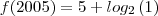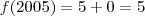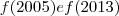por karenblond » Qui Mai 26, 2011 13:34
por karenblond » Qui Mai 26, 2011 13:34
[url][URL=http://imageshack.us/photo/my-images/855/logx.png/]

[/url]
[/url]
-
karenblond
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qua Mar 24, 2010 14:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qui Mai 26, 2011 14:15
por Molina » Qui Mai 26, 2011 14:15
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Claudin » Qui Mai 26, 2011 15:04
por Claudin » Qui Mai 26, 2011 15:04
Agora sim, com o enunciado completo
da pra responder tranquilamente! Basta calcular o
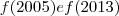
e depois calcular a diferença entre ambos os anos, que você chegará no valor do acréscimo.
Como Molina ja provou para todos.
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2571 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1850 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2735 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5270 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2280 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 [/url]
[/url]
 [/url]
[/url]