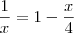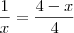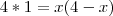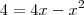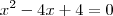Eu consegui montar. Ficou assim:
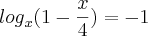
=

invertir a fração
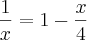
passei o "x" multiplicando e caí em uma equação do segundo grau

coloquei o "x" em evidência
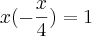
 e multipliquei por (-1)
e multipliquei por (-1)
só que não confere no gabarito. Eu não estou conseguindo resolver quando tem que achar a base.
Podem por favor me ajudar?
Obrigada e no aguardo
(fonte: Matemática aula por aula vol. único., pág. 157, Benigno Barreto Filho e Claudio Xavier da Silva)