Vamos interpretar o enunciado:
A soma de dois números reais é 7:
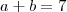 A soma dos seus logaritmos na base 100 é
A soma dos seus logaritmos na base 100 é 
:
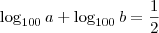
Agora vamos trabalhar com essas informações. A primeira equação não há muito o que fazer, já a segunda pode ser melhorada:
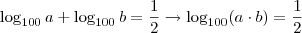
Lembrando a definição de logaritmos (

, com as restrições):

Então temos duas equações:


Primeiro modo:
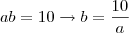
Substituindo na segunda:
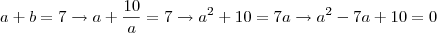
Posso fazer isso pois é certeza que

. Então:

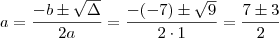
Respostas:

e

ou

e

.
Segundo modo:
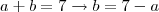
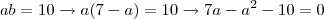
Multiplicando por

:
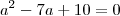
Veja que são meios equivalentes de se chegar na mesma resposta.
Agora entra a importância do módulo.
Módulo quer dizer distância. Módulo entre dois números quer dizer a distância entre eles na reta real. Note que a distância de 5 até 2 é 3, e a distância de 2 até 5 também é 3, porém o que muda é o sentido, simbolizado pelo sinal negativo quando vamos no sentido contrário (ou seja, de 5 para 2). Assim:

Distância é sempre um número
positivo, ou seja, um
número absoluto.
Alternativa D.



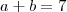
 :
: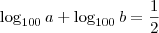
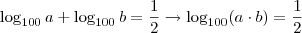
 , com as restrições):
, com as restrições):


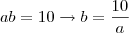
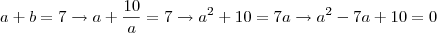
 . Então:
. Então:
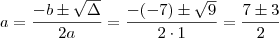
 e
e  ou
ou  e
e  .
.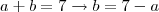
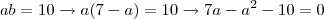
 :
: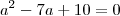







 .
.
 :
: