 por Angelica Abdalla » Ter Jul 12, 2011 21:33
por Angelica Abdalla » Ter Jul 12, 2011 21:33
Boa noite a todos,
Vou colocar o problema e a resoluçaõ que fiz. Vcs podem ver se aonde errei?
PROBLEMA:
Em dois vasos cilíndricos, de eixo vertical, há água até a mesma altura; um dos vasos tem raio 30 cm e o outro 45 cm. Qual é o volume de água que deve ser passado do vaso de menor raio para o outro a fim de que surja uma diferença de 26 cm entre os níveis da água num e noutro vaso?
1) Escreva as equações que correspondem à situação exposta no problema (e que, portanto, permita resolvê-lo), explicando claramente quais são os elementos envolvidos e qual o raciocínio usado para estabelecer tal equação.
2) Resolva as equações para obter a resposta à pergunta posta no problema.
Resolução:
Para resolvermos esse problema, vamos utilizar os conhecimentos de Geometria Espacial, sobre cilindros, no qual aplica-se no 2? ano do Ensino Médio.
Sejam R um círculo contido num plano ? e (XY) ? um segmento de uma reta s concorrente com ?. Denominamos Cilindro o conjunto dos pontos dos segmentos paralelos e congruentes a (XY) ? que têm uma extremidade em R e que estão num mesmo semi-espaço determinado por ?.
Para encontrarmos o volume do cilindro, precisamos conhecer o raio r de sua base, em vez que o volume é dado por:
V_cilindro=( área da base)×(altura)
Sabendo-se que a área da base de um cilindro é A_base=?r^2, logo, temos que o raio do cilindro é 30 cm.
Calculando a Área da base do primeiro cilindro:
A_base=??30?^2
A_base=900? cm²
Calculando o Volume:
Sabendo-se que para calcular o volume, utilizamos a seguinte fórmula:
V_cilindro=( área da base)×(altura)
Logo:
V_cilindro=900?.h cm³
Sabendo-se que a área da base de um cilindro é A_base=?r^2, logo, temos que o raio do segundo cilindro é 45 cm.
Calculando a Área da base do segundo cilindro:
A_base=??45?^2
A_base=2025? cm²
Calculando o Volume do segundo cilindro:
V_cilindro=( área da base)×(altura)
Logo:
V_cilindro=2025?.h cm³
Sabemos que h é a altura inicial dos dois cilindros
V_1, significa o volume inicial do primeiro cilindro: 900?h cm³
V_2, significa o volume inicial do segundo cilindro: 2025?h cm³
Chamaremos x o decréscimo do nível no primeiro vaso
e y acréscimo do nível no segundo vaso.
? V?_1', significa o volume do primeiro cilindro após a passagem do líquido: 900?(h-x)cm³
V_2', significa o volume do segundo cilindro após a passagem do líquido: 2025?(h+y) cm³
Logo:
V_1+V_2=V_1'+V_2'
Sendo que V_1=900? e V_1=900(h-x)volume após a passagem do líquido;
900?h+2025?h=900?(h-x)+2025?(h+y)
900?h+2025?h=900?h-900?x+2025?h+2025?y
900?h+2025?h-900?h-2025?h=-900?x+2025?y
900?x=2025?y
Sabendo-se que x+y=26, e substituindo o x teremos
x+y=26 ? x=26-y
900?x=2025?y ,simplificando ambos por 225 obteremos
4x=9y ? 4x/9=y
Resolvendo este sistema:
x=26-4x/9?9x/9=234/9-4x/9
9x+4x=234
13x=234
x=234/13
x=18 cm
Agora sabemos quanto vale o x, Substituindo na equação acima:
x=26-y
18=26-y
18-26=-y
-8=-y (×-1)
y=8 cm
Encontramos o valor de x e y e substituindo-os obteremos o valor do volume da água que sairá do recipiente de menor raio para o outro;
900?x cm³=2025?ycm³
900?×18=2025?×8
16.200? cm³=16200? cm³
Resposta: Podemos concluir que o volume de água que deve ser passado do cilindro de menor raio para o outro a fim de que surja uma diferença de 26 cm corresponde a 16200? cm³


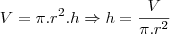
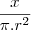 corresponderá ao impacto que um volume x terá no nível da água, correto?
corresponderá ao impacto que um volume x terá no nível da água, correto?
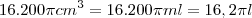


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
