 por Rafael16 » Sex Ago 17, 2012 21:33
por Rafael16 » Sex Ago 17, 2012 21:33
Boa noite pessoal!
(Ufes) Uma produtora pretende lançar um filme em fita de vídeo e prevê uma venda de 20.000 cópias. O custo fixo de produção do filme foi R$150.000,00 e o custo por unidade foi de R$20,00 (fita virgem, processo de copiar e embalagem). Qual o preço mínimo que deverá ser cobrado por fita, para não haver prejuízo?
a) R$ 20,00
b) R$ 22,50
c) R$ 25,00
d) R$ 27,50
e) R$ 35,00
Minha dúvida é na hora de montar a função do custo da produção do filme.
Bom, se a produtora gastou R$150000,00, então o gráfico irá cortar no ponto (0,-150000), pois se ele gastou, ficou negativo.
E pra produzir cada fita, ela gasta R$20,00, então seria negativa também, pois esta gastando(-20x).
Então a função do custo ficaria C(x) = -20x - 150000 (A medida que iria produzindo, o gráfico iria decaindo)
A função da venda seria V(x)=ax
Para não ter prujuízo:
ax = -20x - 150000
x = -27,5
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por DanielFerreira » Sex Ago 17, 2012 21:56
por DanielFerreira » Sex Ago 17, 2012 21:56
Rafael,
pensei da seguinte maneira:
A produtora gastou R$ 150.000,00 pela produção do filme e para fazer as cópias ela gastou mais R$ 400.000,00 [20 X 20.000(cópias)].
Portanto, R$ 150.000,00 + R$ 400.000,00 =
R$ 550.000,00 Para que ela não tenha prejuízo, deverá vender as 20.000 fitas por no mínimo o valor que foi gasto, isto é, R$ 550.000,00.
O valor de cada fita foi R$ k,00, Daí:

Espero ter ajudado.
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por e8group » Sex Ago 17, 2012 21:59
por e8group » Sex Ago 17, 2012 21:59
Boa noite . Veja que o custo total
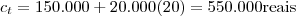
.
Agora seja
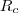
uma função que denota o retorno de capital em função do número de fitas vendidas e o valor relativo a elas .
Assim ,temos :

,onde n é o número de fitas e x seu valor .
A proposito para não haver prejuizo temos que
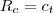
e como há uma previsão de vendas de 20 mil filmes temos que ,

,donde

.
Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




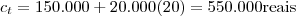 .
.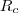 uma função que denota o retorno de capital em função do número de fitas vendidas e o valor relativo a elas .
uma função que denota o retorno de capital em função do número de fitas vendidas e o valor relativo a elas .  ,onde n é o número de fitas e x seu valor .
,onde n é o número de fitas e x seu valor .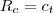 e como há uma previsão de vendas de 20 mil filmes temos que ,
e como há uma previsão de vendas de 20 mil filmes temos que ,  ,donde
,donde  .
.