Lei de Charles e Gay-Lussac

[LuizCarlos]

Olá pessoal, estou estuando química, comportamento físico dos gases, tem uma parte nesse capítulo que explica a lei de Charles e Gay-Lussac, o livro mostra dois gráficos, em que o volume é mantido constante, e a pressão e temperatura variam, porém o livro fala que quando a temperatura está em graus Celsius, pressão e temperatura não são grandezas diretamente proporcionais, mas quando a temperatura está em Kelvim, pressão e temperatura são duas grandezas diretamente proporcionais! mas gostaria de saber como é provado isso matematicamente, pois não estou conseguindo entender esses dois gráficos. Tirei uma foto com o celular dos gráficos, espero que vocês consigam visualizar.

DSC00003_mini.jpg (16.29 KiB) Exibido 2774 vezes

[Lucio Carvalho]

Olá LuizCarlos,
Como podemos ver, o segundo gráfico é uma reta que passa pela origem, o que faz com a pressão e a temperatura sejam diretamente proporcionais, ou seja,

Por exemplo, quando a temperatura em graus Kelvin duplica, a pressão também duplica.
Devemos notar que o 0 kelvin é o zero absoluto e corresponderia a uma pressão igual a zero!

No primeiro gráfico temos uma reta que não passa pela origem. Isso acontece porque 0 ºC não é o zero absoluto e por isso não corresponde a uma pressão igual a zero!

Em termos matemáticos, as duas retas representam funções afins, mas a equação da primeira é do tipo

enquanto que a equação da segunda é do tipo .

Espero ter ajudado!

[LuizCarlos]

Olá LuizCarlos,
Como podemos ver, o segundo gráfico é uma reta que passa pela origem, o que faz com a pressão e a temperatura sejam diretamente proporcionais, ou seja,

Por exemplo, quando a temperatura em graus Kelvin duplica, a pressão também duplica.
Devemos notar que o 0 kelvin é o zero absoluto e corresponderia a uma pressão igual a zero!

No primeiro gráfico temos uma reta que não passa pela origem. Isso acontece porque 0 ºC não é o zero absoluto e por isso não corresponde a uma pressão igual a zero!

Em termos matemáticos, as duas retas representam funções afins, mas a equação da primeira é do tipo

enquanto que a equação da segunda é do tipo .

Espero ter ajudado!

Obrigado Lúcio Carvalho, estarei lendo com atenção o que você explicou, para conseguir entender! sou muito agradecido pela ajuda, abraço amigo.

[LuizCarlos]

Olá LuizCarlos,
Como podemos ver, o segundo gráfico é uma reta que passa pela origem, o que faz com a pressão e a temperatura sejam diretamente proporcionais, ou seja,

Por exemplo, quando a temperatura em graus Kelvin duplica, a pressão também duplica.
Devemos notar que o 0 kelvin é o zero absoluto e corresponderia a uma pressão igual a zero!

No primeiro gráfico temos uma reta que não passa pela origem. Isso acontece porque 0 ºC não é o zero absoluto e por isso não corresponde a uma pressão igual a zero!

Em termos matemáticos, as duas retas representam funções afins, mas a equação da primeira é do tipo

enquanto que a equação da segunda é do tipo .

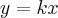
Espero ter ajudado!

Olá Lúcio, entendi algumas coisas que você explicou, porém fiquei em dúvidas em algumas, por exemplo: você diz que no segundo gráfico, devemos notar que o 0 Kelvin é o zero absoluto e corresponde a uma pressão igual a zero!
Fiz uma tabela com valores referente a pressão e temperatura: coloquei o primeiro valor de pressão digamos p1 sendo 0 (zero), e o primeiro valor de temperatura digamos t1 sendo 1, supondo que a temperatura dobre para 2, a pressão também deveria dobrar, visto que são grandezas diretamente proporcionais, mas nesse caso como a pressão é 0(zero) 2.0 = 0, percebe-se que sempre a pressão será 0 (zero). Nesse caso até a razão entre as grandezas será diferente. Gostaria de entender o seguinte também, no segundo gráfico a reta passa pela origem (0,0), então a reta começa da origem e vai subindo, ou começa da origem e também pode ir decrescendo, ou ela pode começar de qualquer valor para pressão e temperatura, mas obrigatoriamente ela tem que passar pela origem! não estou conseguindo entender essas dúvidas!

Você disse que no primeiro gráfico, a reta representa uma função afim, porém ela é do tipo y = k.x + b, esse b é o valor em que a reta corta o eixo y né isso, mas como consigo encontrar essa equação, utilizando valores para pressão e para temperatura, como exemplo.

Como consigo chegar na equação referente ao segundo gráfico, y = k.x , colocando valores para pressão e para temperatura.
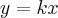