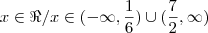por Rafael16 » Qui Jul 05, 2012 12:01
por Rafael16 » Qui Jul 05, 2012 12:01
Na inequação
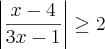
Para (I):
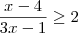
Para (II):
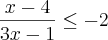
Depois faz a UNIÃO das soluções de cada inequação que fica
S = {
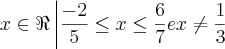
}
Na inequação
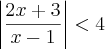
A solução é
S= {
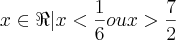
}
O que eu não entendi foi que na primeira inequação, para achar a solução, usa-se a UNIÃO, e na segunda inequação usa-se a INTERSECÇÃO.Por que não pode usar união?
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Qui Jul 05, 2012 13:20
por Russman » Qui Jul 05, 2012 13:20
Para a primeira equação, ou
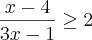
ou
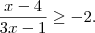
Da primeira,
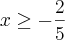
. E da segunda,
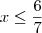
.
Assim, se você desenhar os intervalos vera que se unem de forma que
![{x \in \Re / x \in [ -\frac{2}{5} , \frac{1}{3}) \cup (\frac{1}{3} ,\frac{6}{7}]} {x \in \Re / x \in [ -\frac{2}{5} , \frac{1}{3}) \cup (\frac{1}{3} ,\frac{6}{7}]}](/latexrender/pictures/45484fb6cdc689ccbcdaeb82ec959770.png)
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Jul 05, 2012 13:33
por Russman » Qui Jul 05, 2012 13:33
Na segunda as soluções são
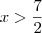
e
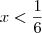
.
Unindo os intervalos, temos
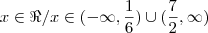
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7386 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- inequação modular
por manuoliveira » Dom Ago 22, 2010 22:30
- 1 Respostas
- 3471 Exibições
- Última mensagem por Dan

Seg Ago 23, 2010 15:38
Álgebra Elementar
-
- Inequação modular
por scggomes » Qui Abr 21, 2011 17:22
- 3 Respostas
- 3204 Exibições
- Última mensagem por MarceloFantini

Qui Abr 21, 2011 20:54
Cálculo: Limites, Derivadas e Integrais
-
- Inequação Modular
por Rafael16 » Qui Mar 08, 2012 20:24
- 2 Respostas
- 2414 Exibições
- Última mensagem por Rafael16

Qui Mar 08, 2012 21:21
Funções
-
- inequação modular
por haiashi » Qua Jun 06, 2012 00:33
- 0 Respostas
- 1545 Exibições
- Última mensagem por haiashi

Qua Jun 06, 2012 00:33
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

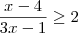
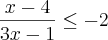
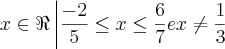 }
}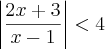
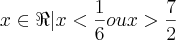 }
}

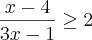
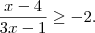
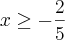 . E da segunda,
. E da segunda, 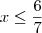 .
.![{x \in \Re / x \in [ -\frac{2}{5} , \frac{1}{3}) \cup (\frac{1}{3} ,\frac{6}{7}]} {x \in \Re / x \in [ -\frac{2}{5} , \frac{1}{3}) \cup (\frac{1}{3} ,\frac{6}{7}]}](/latexrender/pictures/45484fb6cdc689ccbcdaeb82ec959770.png) .
.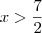 e
e 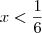 .
.