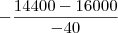por PeterHiggs » Sex Mai 25, 2012 22:24
por PeterHiggs » Sex Mai 25, 2012 22:24
Considere x,y
tais que 3x - y = 20. O menor valor de

é:
a) 2
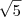
b) 2

c) 2

d) 4
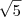
e) 4
 Resposta:
Resposta: Alternativa b)
* Bom, aqui está o que eu tentei fazer, mas obviamente não fechou com o resultado:
3x - y = 20
y = 3x - 20;
Substituindo na raiz:



O valor sob a raiz sera o menor possível no vértice da parábola descrita pela função

, já que o coeficiente de

é positivo (ou seja, concavidade pra cima, e valor mínimo).
yv =

;
yv =

;
yv =

;
yv = 4;
Raiz de 4 é 2. Não fecha com nenhuma das alternativas. Alguém pode me indicar o caminho certo? Qual seria o menor valor assumido pelo expressão na raiz?
-
PeterHiggs
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Mai 25, 2012 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por PeterHiggs » Sáb Mai 26, 2012 16:09
por PeterHiggs » Sáb Mai 26, 2012 16:09
Ops, pessoal, foi mal. Cometi um ridículo equívoco com relação ao cálculo do yv na equação do 2° grau.
Simplifiquei a equação

para

, e daí calculei o yv. Não sei porque fiz isso...
Me desculpem pela distração!
 Resolução correta:
Resolução correta:3x - y = 20
y = 3x - 20;
Substituindo na raiz:



O valor sob a raiz sera o menor possível no vértice da parábola descrita pela função

, já que o coeficiente de

é positivo (ou seja, concavidade pra cima, e valor mínimo).
yv =

;
yv =

;
yv = 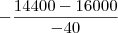 yv = 40;
yv = 40;Raiz de 40 é 2

.
Alternativa b)
-
PeterHiggs
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Mai 25, 2012 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual é o menor e o maior valor de x na expressão
por andersontricordiano » Seg Out 03, 2011 16:56
- 1 Respostas
- 3939 Exibições
- Última mensagem por MarceloFantini

Seg Out 03, 2011 21:10
Trigonometria
-
- menor valor de x
por stuart clark » Sáb Mai 28, 2011 00:41
- 0 Respostas
- 1792 Exibições
- Última mensagem por stuart clark

Sáb Mai 28, 2011 00:41
Trigonometria
-
- Qual deverá ser menor valor da força F
 por andersontricordiano » Qui Dez 15, 2011 11:44
por andersontricordiano » Qui Dez 15, 2011 11:44
- 5 Respostas
- 4599 Exibições
- Última mensagem por Fabricio dalla

Sex Dez 23, 2011 15:57
Mecânica
-
- [Geometria] O menor valor possível para soma.
 por my2009 » Ter Fev 09, 2016 10:59
por my2009 » Ter Fev 09, 2016 10:59
- 1 Respostas
- 4574 Exibições
- Última mensagem por Baltuilhe

Sáb Fev 20, 2016 19:27
Geometria
-
- Isolar uma variável numa equação de grau 3
por KleinIll » Dom Abr 24, 2016 16:37
- 0 Respostas
- 7156 Exibições
- Última mensagem por KleinIll

Dom Abr 24, 2016 16:37
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
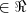 tais que 3x - y = 20. O menor valor de
tais que 3x - y = 20. O menor valor de  é:
é: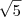


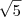




 , já que o coeficiente de
, já que o coeficiente de  é positivo (ou seja, concavidade pra cima, e valor mínimo).
é positivo (ou seja, concavidade pra cima, e valor mínimo). ;
; ;
; ;
;

 , e daí calculei o yv. Não sei porque fiz isso...
, e daí calculei o yv. Não sei porque fiz isso...