Bom dia.
Segundo a minha interpretação do enunciado, primeiramente terás de achar as raízes da parábola. Ou seja, achar os zeros: f(x)=0.
Designemos por x1 e x2 as raízes encontradas.
De seguida, tens de encontrar a ordenada no ponto em que a parábola toca o eixo Oy, ou seja, f(0), pois quando a função intersecta o eixo oy, o x tem de ser obrigatoriamente igual a 0.
Sendo assim,

.
Quanto ao valor de B, tens de determinar o valor mínimo e o minimizante(abcissa do mínimo). Para tal, poderás utilizar a derivada da função f.
Como pede a razão entre o mínimo e o minimizante, B=

.
Depois é só somar A com B.
Espero ter ajudado.
Obrigado!
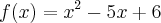 . Sendo A a soma de suas raízes reais multiplicada pelo valor
. Sendo A a soma de suas raízes reais multiplicada pelo valor

 .
. .
.
 .
.
 :
: