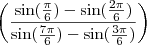por jamiel » Sáb Jul 02, 2011 04:23
por jamiel » Sáb Jul 02, 2011 04:23
Calcule o valor da expressão(para x = pi/6):
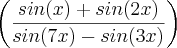
Eu fui resolvendo pelas formulas de adição e subtração, mas não deu o resultado do gabarito. Então, fui tentando resolver, de fato, eu fiz, mas não entendi muito bem o "porquê"
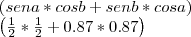
De fato, se eu cortar sen a e cos a, fico com:
![\left(\frac{1}{2}+0.87 \right)
\left(\frac{\sqrt[]{3}+1}{2} \right) \left(\frac{1}{2}+0.87 \right)
\left(\frac{\sqrt[]{3}+1}{2} \right)](/latexrender/pictures/7aceb417f81df18a922a8357ce2e29d3.png)
No denominador, eu tenho

De fato, se eu cortar 0 e -0.87, eu fico com

Por fim,
![\left(\frac{\frac{\sqrt[]{3}+1}{2}}{-\frac{3}{2}} \right)
\left(\frac{-\sqrt[]{3}-1}{3} \right) \left(\frac{\frac{\sqrt[]{3}+1}{2}}{-\frac{3}{2}} \right)
\left(\frac{-\sqrt[]{3}-1}{3} \right)](/latexrender/pictures/a69491fc07ba0628e7c60bf81105f59a.png)
Agradeço qualquer ajuda, desde já!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Setor circular
 por DanielFerreira » Sex Mar 04, 2011 11:08
por DanielFerreira » Sex Mar 04, 2011 11:08
- 1 Respostas
- 3963 Exibições
- Última mensagem por LuizAquino

Sex Mar 04, 2011 12:08
Geometria Plana
-
- Setor Circular
 por Arkanus Darondra » Qua Fev 01, 2012 18:42
por Arkanus Darondra » Qua Fev 01, 2012 18:42
- 6 Respostas
- 5753 Exibições
- Última mensagem por Arkanus Darondra

Dom Fev 05, 2012 09:20
Geometria Espacial
-
- Permutação circular
por anfran1 » Dom Nov 17, 2013 10:53
- 0 Respostas
- 1084 Exibições
- Última mensagem por anfran1

Dom Nov 17, 2013 10:53
Análise Combinatória
-
- pista circular
por adauto martins » Seg Set 29, 2014 15:45
- 1 Respostas
- 1172 Exibições
- Última mensagem por adauto martins

Sex Jul 22, 2016 17:04
Cálculo: Limites, Derivadas e Integrais
-
- Calculo circular
por lucastrmendes » Sex Mai 08, 2015 16:07
- 0 Respostas
- 2249 Exibições
- Última mensagem por lucastrmendes

Sex Mai 08, 2015 16:07
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
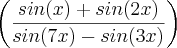
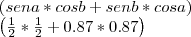
![\left(\frac{1}{2}+0.87 \right)
\left(\frac{\sqrt[]{3}+1}{2} \right) \left(\frac{1}{2}+0.87 \right)
\left(\frac{\sqrt[]{3}+1}{2} \right)](/latexrender/pictures/7aceb417f81df18a922a8357ce2e29d3.png)


![\left(\frac{\frac{\sqrt[]{3}+1}{2}}{-\frac{3}{2}} \right)
\left(\frac{-\sqrt[]{3}-1}{3} \right) \left(\frac{\frac{\sqrt[]{3}+1}{2}}{-\frac{3}{2}} \right)
\left(\frac{-\sqrt[]{3}-1}{3} \right)](/latexrender/pictures/a69491fc07ba0628e7c60bf81105f59a.png)