 por Jonatan » Qua Jul 28, 2010 13:24
por Jonatan » Qua Jul 28, 2010 13:24
Determinar o domínio da função:
![f(x)= \sqrt[2]{\frac{(1-x)({x}^{2}-4)}{2x-1}} f(x)= \sqrt[2]{\frac{(1-x)({x}^{2}-4)}{2x-1}}](/latexrender/pictures/d2a94274c8ad5615ce947edfd0dbd721.png)
Estou sem o gabarito. Gostaria de conferir se resolvi corretamente.
O meu conjunto domínio, após ter estudado o sinal da função, através do Teorema de Bolzano, foi o seguinte:
D[f(x)] = {

|
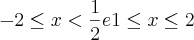
}
Confere?
-
Jonatan
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Jun 16, 2010 13:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Jul 28, 2010 14:51
por MarceloFantini » Qua Jul 28, 2010 14:51
Confere, sua resposta está certa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3249 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2883 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- Determinação de um exercício contendo derivada de uma função
por vmendes » Sex Mai 30, 2014 22:12
- 0 Respostas
- 761 Exibições
- Última mensagem por vmendes

Sex Mai 30, 2014 22:12
Cálculo: Limites, Derivadas e Integrais
-
- [Domínio da Função] A função abaixo é definida f(x)=x²-3x
por Tiago Neto » Qui Mai 30, 2013 20:58
- 0 Respostas
- 1768 Exibições
- Última mensagem por Tiago Neto

Qui Mai 30, 2013 20:58
Funções
-
- dominio da funçao
por Thassya » Sex Mai 29, 2009 11:26
- 4 Respostas
- 5161 Exibições
- Última mensagem por Marcampucio

Dom Mai 31, 2009 18:58
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)= \sqrt[2]{\frac{(1-x)({x}^{2}-4)}{2x-1}} f(x)= \sqrt[2]{\frac{(1-x)({x}^{2}-4)}{2x-1}}](/latexrender/pictures/d2a94274c8ad5615ce947edfd0dbd721.png)
 |
|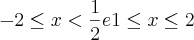 }
}
![f(x)= \sqrt[2]{\frac{(1-x)({x}^{2}-4)}{2x-1}} f(x)= \sqrt[2]{\frac{(1-x)({x}^{2}-4)}{2x-1}}](/latexrender/pictures/d2a94274c8ad5615ce947edfd0dbd721.png)
 |
|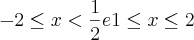 }
}


 .
.



