 por Pessoa Estranha » Qui Set 25, 2014 17:54
por Pessoa Estranha » Qui Set 25, 2014 17:54
Olá!
Gostaria de ajuda para provar que a seguinte função é bijetora:
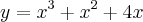
Não estou conseguindo. Comecei tentando provar que é injetora, mas não consigo chegar em nada. Acho que o método que estou tentando usar não está ajudando. Tem alguma forma simples para resolver?
Podem, por favor, me ajudar?
Muito Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Qui Set 25, 2014 18:38
por adauto martins » Qui Set 25, 2014 18:38
tomemos (x(1)de y(1)e x(2)de y(2)
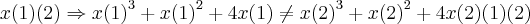
,mostramos elementos distintos dos dois conj. terao imagens distintas,o q. prova a injeçao;agora podemos ver q. todo e qquer x tera sempre um y,e q. se tomarmos dois elementos de y(1) teremos os mesmos valores em y(2),ou seja os conj.imagens serao iguais,o q. prova a sobrejeçao...logo y e injetiva e sobrejetiva,o q.implica y injetiva
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Pessoa Estranha » Sex Set 26, 2014 10:55
por Pessoa Estranha » Sex Set 26, 2014 10:55
Olá! Muito Obrigada!
Não entendi muito bem o que você fez em:
adauto martins escreveu:tomemos (x(1)de y(1)e x(2)de y(2)
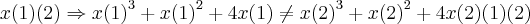
Por favor, pode explicar?
Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Sex Set 26, 2014 12:06
por adauto martins » Sex Set 26, 2014 12:06
meu caro pessoa estranha,
e o LATEX, nao consigo escrever certo...sai,mas num e bom...no caso,tomemos x1 diferente de x2 q. implica em suas imagens(y1 e y2) diferentes,caso de ser injetiva...no caso da sobrejetiva,mostrar-se q. para qquer y(imagem) existe um unico x do conj.dominio tal q. y=f(x),ou seja se tomarmos imagens iguais teremos dominios iguais o q. mostra q. os conjuntos domino e imagem teem os mesmo elementos,ou melhor sao iguais...vamos la...se tomarmos y=k,k um real,entao existe x,tal q. x e soluçao da equaçao dada,(x^3)+(x^2)+4x=k...obteremos x=f(k)...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Pessoa Estranha » Sáb Set 27, 2014 13:02
por Pessoa Estranha » Sáb Set 27, 2014 13:02
Está bem. Muito obrigada pela ajuda!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções - provar propriedade
por emsbp » Sáb Jul 07, 2012 17:59
- 2 Respostas
- 1646 Exibições
- Última mensagem por emsbp

Dom Jul 08, 2012 18:27
Funções
-
- Funções impares- como provar
por Thayna Santos » Seg Mar 16, 2015 12:10
- 1 Respostas
- 1903 Exibições
- Última mensagem por adauto martins

Seg Mar 16, 2015 15:41
Funções
-
- Provar se é par
por stalone » Seg Dez 21, 2009 23:29
- 5 Respostas
- 3216 Exibições
- Última mensagem por stalone

Seg Dez 13, 2010 13:07
Desafios Difíceis
-
- Provar que ||u|| > 0
por 0 kelvin » Qui Mar 24, 2011 20:35
- 2 Respostas
- 1972 Exibições
- Última mensagem por 0 kelvin

Qui Mar 24, 2011 21:16
Geometria Analítica
-
- Provar
por scggomes » Sex Abr 15, 2011 16:38
- 8 Respostas
- 5944 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 16, 2011 15:56
Cálculo para Funções de Uma Variável Real I
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
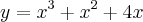


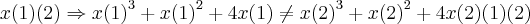 ,mostramos elementos distintos dos dois conj. terao imagens distintas,o q. prova a injeçao;agora podemos ver q. todo e qquer x tera sempre um y,e q. se tomarmos dois elementos de y(1) teremos os mesmos valores em y(2),ou seja os conj.imagens serao iguais,o q. prova a sobrejeçao...logo y e injetiva e sobrejetiva,o q.implica y injetiva
,mostramos elementos distintos dos dois conj. terao imagens distintas,o q. prova a injeçao;agora podemos ver q. todo e qquer x tera sempre um y,e q. se tomarmos dois elementos de y(1) teremos os mesmos valores em y(2),ou seja os conj.imagens serao iguais,o q. prova a sobrejeçao...logo y e injetiva e sobrejetiva,o q.implica y injetiva
