


 em geral significa função inversa de
em geral significa função inversa de  .Agora
.Agora 
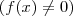 é apenas um número , o qual varia de acordo com uma regra , lei de associação da função chamada
é apenas um número , o qual varia de acordo com uma regra , lei de associação da função chamada  . Mais precisamente
. Mais precisamente  é o inverso multiplicativo de
é o inverso multiplicativo de  diferente de zero ; e também denotamos ele por
diferente de zero ; e também denotamos ele por ![[f(x)]^{-1} [f(x)]^{-1}](/latexrender/pictures/5965afd864edd417f09c34550b621617.png) .
.  é o inverso multiplicativo de
é o inverso multiplicativo de  (3^{-1} \cdot 3 = 1 ) . Agora seja
(3^{-1} \cdot 3 = 1 ) . Agora seja 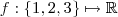 dada pela lei de associação :
dada pela lei de associação :  . Note que
. Note que  e
e  ; logo
; logo ![[f(1)]^{-1} [f(1)]^{-1}](/latexrender/pictures/281a36bb5a8aa2cdc9413d2ded2c77e2.png) é o inverso multiplicativo de
é o inverso multiplicativo de  . Tome cuidado ! Não confunda
. Tome cuidado ! Não confunda  com
com ![[f(x)]^{-1}= \frac{1}{f(x)} [f(x)]^{-1}= \frac{1}{f(x)}](/latexrender/pictures/7daaf0843e3ce7dff9767516948bc5df.png)
 não é função ! Muitas vezes por simplicidade , dizemos a função
não é função ! Muitas vezes por simplicidade , dizemos a função  ... ao invés de dizer função
... ao invés de dizer função  definida pela regra de associação
definida pela regra de associação  a qual estabelece uma relação entre elementos de dois conjuntos . (isto pode gerar muitas dúvidas )
a qual estabelece uma relação entre elementos de dois conjuntos . (isto pode gerar muitas dúvidas )  é uma função real de uma variável .Ou seja , uma função
é uma função real de uma variável .Ou seja , uma função  ) a qual a cada elemento
) a qual a cada elemento  em
em  faz corresponder um
faz corresponder um  em
em  . Ora , se B é um subconjunto dos números reais e
. Ora , se B é um subconjunto dos números reais e  está em B , então f(x) só pode ser um número real .
está em B , então f(x) só pode ser um número real . 
 em geral significa função inversa de
em geral significa função inversa de  .Agora
.Agora 
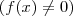 é apenas um número , o qual varia de acordo com uma regra , lei de associação da função chamada
é apenas um número , o qual varia de acordo com uma regra , lei de associação da função chamada  . Mais precisamente
. Mais precisamente  é o inverso multiplicativo de
é o inverso multiplicativo de  diferente de zero ; e também denotamos ele por
diferente de zero ; e também denotamos ele por ![[f(x)]^{-1} [f(x)]^{-1}](/latexrender/pictures/5965afd864edd417f09c34550b621617.png) .
.  é o inverso multiplicativo de
é o inverso multiplicativo de  (3^{-1} \cdot 3 = 1 ) . Agora seja
(3^{-1} \cdot 3 = 1 ) . Agora seja 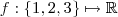 dada pela lei de associação :
dada pela lei de associação :  . Note que
. Note que  e
e  ; logo
; logo ![[f(1)]^{-1} [f(1)]^{-1}](/latexrender/pictures/281a36bb5a8aa2cdc9413d2ded2c77e2.png) é o inverso multiplicativo de
é o inverso multiplicativo de  . Tome cuidado ! Não confunda
. Tome cuidado ! Não confunda  com
com ![[f(x)]^{-1}= \frac{1}{f(x)} [f(x)]^{-1}= \frac{1}{f(x)}](/latexrender/pictures/7daaf0843e3ce7dff9767516948bc5df.png)
 não é função ! Muitas vezes por simplicidade , dizemos a função
não é função ! Muitas vezes por simplicidade , dizemos a função  ... ao invés de dizer função
... ao invés de dizer função  definida pela regra de associação
definida pela regra de associação  a qual estabelece uma relação entre elementos de dois conjuntos . (isto pode gerar muitas dúvidas )
a qual estabelece uma relação entre elementos de dois conjuntos . (isto pode gerar muitas dúvidas )  é uma função real de uma variável .Ou seja , uma função
é uma função real de uma variável .Ou seja , uma função  ) a qual a cada elemento
) a qual a cada elemento  em
em  faz corresponder um
faz corresponder um  em
em  . Ora , se B é um subconjunto dos números reais e
. Ora , se B é um subconjunto dos números reais e  está em B , então f(x) só pode ser um número real .
está em B , então f(x) só pode ser um número real . 
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

