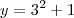por Sobreira » Sex Nov 16, 2012 16:27
por Sobreira » Sex Nov 16, 2012 16:27
Olá amigos,
Tenho uma dúvida, que está me travando no prosseguimento dos meus estudos:
Não sei identificar quando uma função é composta.
Por exemplo:
![y=\sqrt[]{x}.sen x y=\sqrt[]{x}.sen x](/latexrender/pictures/9d865190c07c423023adbdaf5fb93af0.png)
Esta função é composta???
Mas não gostaria de respostas restritas à este exemplo, gostaria de mais exemplos e formas de como identificar (para todo caso) uma função composta.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Sex Nov 16, 2012 17:08
por MarceloFantini » Sex Nov 16, 2012 17:08
Isto não é uma composição de funções, isto é um produto. Para enxergar melhor composição de funções, primeiro você precisa ter em mente todas as funções elementares, como:

Não são "todas", mas é uma boa lista. Lembre-se que em

temos que

é real, logo isso inclui

,

,
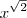
,

, etc.
Segundo, qual é a regra de composição de funções usual? Você coloca uma função "dentro" da outra, da seguinte forma:
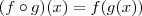
. Vamos tomar o caso

e

. Então
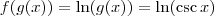
.
Outro exemplo: tome

,
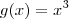
e

. Encontre

. Pela definição dada, isto é

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Sex Nov 16, 2012 19:22
por Sobreira » Sex Nov 16, 2012 19:22
Desculpe,
Mas ainda não consegui entender perfeitamente.
Quando eu verificar uma notação do tipo:
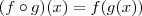
Eu sei que vou ter uma função composta....Agora quando ela vir por exemplo como:
![y=\sqrt[]{x}.sen x y=\sqrt[]{x}.sen x](/latexrender/pictures/9d865190c07c423023adbdaf5fb93af0.png)
tratando de Y e não de f(x) eu ainda não consigo ver.
Pelo pouco que eu entendi...para ser uma função composta é necessário ter uma função elevado a algum expoente???
Desculpa mesmo....mas ainda não consigo diferenciar.
E agora ainda fiquei com a dúvida de como diferenciar uma função produto de uma função composta, além de não ter entendido como detectar de cara uma função composta.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Sex Nov 16, 2012 19:42
por MarceloFantini » Sex Nov 16, 2012 19:42
Você sabe que

e

são duas funções elementares. Uma parece estar "dentro" da outra? Quando eu digo "dentro", quero dizer que a variável da função é algo diferente de

, mais precisamente é uma outra função de

. Não, não é necessário ter uma função elevado a algum expoente, isto mostra que você não entendeu o que eu disse.
Na primeira composição de funções não há qualquer expoente envolvido, a função foi

.
A função dada é produto das funções

e

, logo

.
Para perceber que operações estão sendo feitas, você deve identificar todas as funções elementares envolvidas.
Tome isto como exemplo:

. Quais são as funções elementares envolvidas?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Sex Nov 16, 2012 19:55
por Sobreira » Sex Nov 16, 2012 19:55
Respondendo à sua pergunta, pelo que eu entendi eu vejo que as funções elementares envolvidas são:
 "Uma parece estar "dentro" da outra? Quando eu digo "dentro", quero dizer que a variável da função é algo diferente de
"Uma parece estar "dentro" da outra? Quando eu digo "dentro", quero dizer que a variável da função é algo diferente de  , mais precisamente é uma outra função de
, mais precisamente é uma outra função de  ."
."Gostaria de entender melhor esta parte de sua explicação....
Conseguir enxergar se há "uma função dentro de outra"...Neste exato ponto não consigo entender e acho que se eu conseguir "enxergar" este ponto, aí sim vou sanar minha dúvida satisfatoriamente.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Sex Nov 16, 2012 20:15
por MarceloFantini » Sex Nov 16, 2012 20:15
Você acertou as funções elementares envolvidas. Mais precisamente,

.
Agora, quais são as operações usuais de funções? Soma, subtração, multiplicação, divisão (quando a divisora é diferente de zero) e composição. Se denominarmos
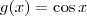
e
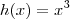
.
Vejamos as expressões de cada uma:
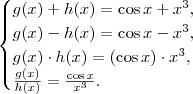
Ora, nenhuma destas expressões correspondem à função dada. Por eliminação, só pode ser composição.
O que eu acabei de fazer foi a maneira grosseira de descobrir quando é composição (neste caso simples).
Para enxergar a composição, pense no seguinte: quando escrevemos
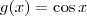
, sabemos que

é um número (real, usualmente), correto? Então qualquer número dentro do domínio, claro, pode ser colocado lá. Além disso, a variável é 'muda', ou seja,

é o mesmo que
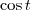
,
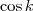
,
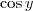
,

,

, e assim em diante (assumindo que estas variáveis não denotem outra coisa).
Portanto, se podemos colocar qualquer número, quero colocar em particular o número igual a
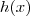
. Assim como avaliamos funções no domínio, como
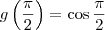
, posso avaliá-la no ponto
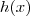
, escrevendo
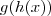
, que tem valor

.
Mas nós temos uma expressão para
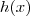
, que é justamente

. Substituindo segue que

. É isto que quero dizer quando uma função está "dentro" da outra. No lugar da variável usual, a variável torna-se uma nova função.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Sáb Nov 17, 2012 00:02
por Sobreira » Sáb Nov 17, 2012 00:02
Consegui ver de forma bastante clara a diferença entre as operações com funções (principalmente a diferença para a função composta).
Agora, uma coisa que reparei (para fazer uma associação), por exemplo, é que quando temos uma função composta temos mais de uma função elementar envolvida com a mesma variável "x" ( um único x), enquanto nas demais operações (soma, subtração, divisão e multiplicação) temos duas variavéis "x".
Por exemplo, nestas operações verificamos duas variavéis "x":
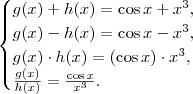
E esta também:
![y=\sqrt[]{x}.sen x y=\sqrt[]{x}.sen x](/latexrender/pictures/9d865190c07c423023adbdaf5fb93af0.png)
Enquanto que quando temos uma função composta temos apenas um "x".
Por exemplo:

.
![y=\sqrt[]{2x+1} y=\sqrt[]{2x+1}](/latexrender/pictures/7692140ab9009acb94457536be429c46.png)
(Aproveitando porque esta função é composta??)
Esta minha observação tem algum fundamento (sentido)? E mais, se tem fundamento....qual a explicação???
Desculpe pela insistência, mas procuro sempre buscar a essência da questão, para entender totalmente o assunto.
Obrigado.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Sáb Nov 17, 2012 08:46
por MarceloFantini » Sáb Nov 17, 2012 08:46
Sua observação tem todo sentido.

A função que disse é uma composição das funções
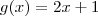
e

, assim

.
Lembre-se que podemos compor quaisquer funções que estejam dentro do domínio da próxima, portanto não é necessário que a variável apareça uma única vez. Considere o exemplo em que

e
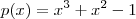
. Então
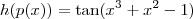
.
Agora, não sei qual é o tipo de explicação que você quer. Isto segue pela definição de composição de funções.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Sáb Nov 17, 2012 15:44
por Sobreira » Sáb Nov 17, 2012 15:44
Bom,
Analisando toda essa nossa discussão e estudando algumas literaturas consegui entender o seguinte, e gostaria que me pudesse me corrigir caso eu esteja errado:
Para pensar numa função composta posso por exemplo, substituir "x"por qualquer número real e verificar se eu obtenho a imagem da função de forma direta, por exemplo:



Nestes casos quando eu substituo o "x"por qualquer número real tenho um cálculo direto (para "x"=3)
y=sen3
y=0.05

y=9

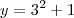
y=10
Enquanto que quando eu tenho uma função composta, o cálculo da imagem da função não acontece de maneira direta, por exemplo:

![y=\sqrt[]{2x+1} y=\sqrt[]{2x+1}](/latexrender/pictures/7692140ab9009acb94457536be429c46.png)
No primeiro caso eu tenho que elevar "x" ao cubo primeiro e
depois calcular o cos deste resultado.
No segundo caso eu tenho que descobrir o valor da expressão 2x+1 primeiro e
depois calcular a raíz quadrada deste resultado.
Está certo este meu raciocínio?
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Desigualdades de funções compostas
por samra » Ter Fev 28, 2012 10:41
- 1 Respostas
- 1424 Exibições
- Última mensagem por LuizAquino

Ter Fev 28, 2012 15:54
Funções
-
- Concavidade de Funções Compostas
por danielfcastro » Seg Jun 10, 2013 20:05
- 0 Respostas
- 1128 Exibições
- Última mensagem por danielfcastro

Seg Jun 10, 2013 20:05
Funções
-
- Funções Compostas e seus domínios
por NinhaH » Ter Jan 04, 2011 11:58
- 2 Respostas
- 3495 Exibições
- Última mensagem por NinhaH

Qui Jan 06, 2011 11:31
Funções
-
- Exemplos de reconhecimento de funções compostas.
por Sobreira » Seg Nov 26, 2012 14:25
- 1 Respostas
- 1646 Exibições
- Última mensagem por MarceloFantini

Seg Nov 26, 2012 19:05
Funções
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3423 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![y=\sqrt[]{x}.sen x y=\sqrt[]{x}.sen x](/latexrender/pictures/9d865190c07c423023adbdaf5fb93af0.png)



 temos que
temos que  é real, logo isso inclui
é real, logo isso inclui  ,
,  ,
, 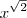 ,
,  , etc.
, etc.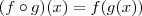 . Vamos tomar o caso
. Vamos tomar o caso  e
e  . Então
. Então 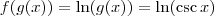 .
. ,
, 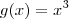 e
e  . Encontre
. Encontre  . Pela definição dada, isto é
. Pela definição dada, isto é  .
.

 e
e  são duas funções elementares. Uma parece estar "dentro" da outra? Quando eu digo "dentro", quero dizer que a variável da função é algo diferente de
são duas funções elementares. Uma parece estar "dentro" da outra? Quando eu digo "dentro", quero dizer que a variável da função é algo diferente de  , mais precisamente é uma outra função de
, mais precisamente é uma outra função de  .
. e
e  , logo
, logo  .
. . Quais são as funções elementares envolvidas?
. Quais são as funções elementares envolvidas?
 .
.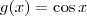 e
e 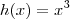 .
.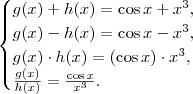
 é o mesmo que
é o mesmo que 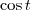 ,
, 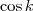 ,
, 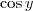 ,
,  ,
,  , e assim em diante (assumindo que estas variáveis não denotem outra coisa).
, e assim em diante (assumindo que estas variáveis não denotem outra coisa).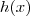 . Assim como avaliamos funções no domínio, como
. Assim como avaliamos funções no domínio, como 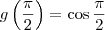 , posso avaliá-la no ponto
, posso avaliá-la no ponto 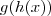 , que tem valor
, que tem valor  .
. . Substituindo segue que
. Substituindo segue que  . É isto que quero dizer quando uma função está "dentro" da outra. No lugar da variável usual, a variável torna-se uma nova função.
. É isto que quero dizer quando uma função está "dentro" da outra. No lugar da variável usual, a variável torna-se uma nova função.![y=\sqrt[]{2x+1} y=\sqrt[]{2x+1}](/latexrender/pictures/7692140ab9009acb94457536be429c46.png) (Aproveitando porque esta função é composta??)
(Aproveitando porque esta função é composta??)
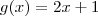 e
e  , assim
, assim  .
.  e
e 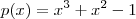 . Então
. Então 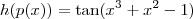 .
.