 intercepta o eixo x nos pontos A e B e, o eixo y no ponto C. A área do triângulo ABC é
intercepta o eixo x nos pontos A e B e, o eixo y no ponto C. A área do triângulo ABC éA) 9
B) 10,5
C) 18
D) 21
E) 42
Tentei dar um valor para o x para descobrir y, mas me compliquei mais. Como posso resolver?
Obrigada.

 intercepta o eixo x nos pontos A e B e, o eixo y no ponto C. A área do triângulo ABC é
intercepta o eixo x nos pontos A e B e, o eixo y no ponto C. A área do triângulo ABC é
 para x real diferente que zero e que intercepta y
para x real diferente que zero e que intercepta y 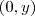 para y real diferente que zero .
para y real diferente que zero .  e
e  , resolva
, resolva  , isto é
, isto é 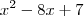 .
.  só calcular
só calcular  para
para  .
.  . Quando vc esboçar o gráfico , considere um ponto
. Quando vc esboçar o gráfico , considere um ponto 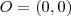 , você verá que a área pode ser expressa por
, você verá que a área pode ser expressa por 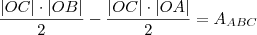 .
.
 daria o mesmo resultado.
daria o mesmo resultado.
 precisará de uns dos ângulos internos para obter a altura relativa a um de seus segmento . Por exemplo , se
precisará de uns dos ângulos internos para obter a altura relativa a um de seus segmento . Por exemplo , se  é altura relativa ao segmento
é altura relativa ao segmento  , teremos que
, teremos que 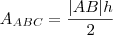 .Mas para isso é necessário pelos um de seus ângulos internos . Mas como
.Mas para isso é necessário pelos um de seus ângulos internos . Mas como 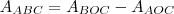 e
e  é perpendicular ao segmentos
é perpendicular ao segmentos 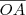 e
e 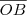 , isto é
, isto é  é altura relativa aos segmentos
é altura relativa aos segmentos 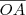 e
e 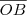 , logo será mais conveniente obter a área deste modo .
, logo será mais conveniente obter a área deste modo . 


Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

