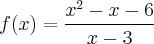
Como determinar algebricamente a imagem desta função, por favor.
Obrigado, galera.

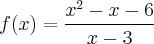

![f : [a,b] \subset \mathbb{R} \longrightarrow \mathbb{R} f : [a,b] \subset \mathbb{R} \longrightarrow \mathbb{R}](/latexrender/pictures/c08dcf6d00d1a4ccbd5694147bb6f91a.png) não pode ter imagem ilimitada , salve em alguns casos onde esta função não é contínua . No caso contínumo a imagem de f será precisamente um intervalo fechado .. Um resultado útil é o seguinte : Dada qualquer
não pode ter imagem ilimitada , salve em alguns casos onde esta função não é contínua . No caso contínumo a imagem de f será precisamente um intervalo fechado .. Um resultado útil é o seguinte : Dada qualquer 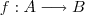 (não necessariamente uma bijeção ) fazemos corresponde uma bijeção
(não necessariamente uma bijeção ) fazemos corresponde uma bijeção 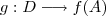 dada por
dada por  , onde
, onde 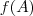 é imagem de
é imagem de  ( a que queremos determinar ) e
( a que queremos determinar ) e 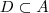 é obtido do seguinte modo :
é obtido do seguinte modo :  em A, vamos dizer que eles são equivalentes(notação
em A, vamos dizer que eles são equivalentes(notação  se
se 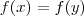 . Esta relação é o que chamamos de relação de equivalence em A . (Ela é reflexiva , simétrica e transitiva ) . Dado
. Esta relação é o que chamamos de relação de equivalence em A . (Ela é reflexiva , simétrica e transitiva ) . Dado 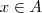 definimos
definimos ![[x]_{\sim} := \{ y \in A ; f(y) = f(x) \} [x]_{\sim} := \{ y \in A ; f(y) = f(x) \}](/latexrender/pictures/c85a75acb17280d283e1504acf113719.png) . Um bom exercício (o qual pode verificar para p qualqer relação de equivalence ) é que duas classes quaisquer
. Um bom exercício (o qual pode verificar para p qualqer relação de equivalence ) é que duas classes quaisquer ![[x]_{\sim} , [y]_{\sim} [x]_{\sim} , [y]_{\sim}](/latexrender/pictures/86f20ad63a46f234038cb6e88d0666c3.png) são disjuntas ou são iguais . Então para cada classe
são disjuntas ou são iguais . Então para cada classe ![[x]_{\sim} [x]_{\sim}](/latexrender/pictures/522ac822e72e2748162dd36cc7c9c00f.png) escolhemos um representante digamos
escolhemos um representante digamos  ... E assim ,D pode ser obtido como o subconunto de A constituidos destes elemenos x .. Então g será injetiva logo uma bijeção e portanto g admirtira uma inversa
... E assim ,D pode ser obtido como o subconunto de A constituidos destes elemenos x .. Então g será injetiva logo uma bijeção e portanto g admirtira uma inversa  e assim sua imagem pode ser efetivamente determinada que e é preisamente o domínio da inversa ... Este seria uma forma 'algebrica' ..as demais são mais 'analiticas ' ... I 'm sorry .... Estou sem tempo e nao conseguir redigir tudo proprieamenrte .. E o modo 2 é a mesma ideia porem mais informal ..
e assim sua imagem pode ser efetivamente determinada que e é preisamente o domínio da inversa ... Este seria uma forma 'algebrica' ..as demais são mais 'analiticas ' ... I 'm sorry .... Estou sem tempo e nao conseguir redigir tudo proprieamenrte .. E o modo 2 é a mesma ideia porem mais informal ..

Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.