 por Rodrigo Tomaz » Sex Fev 19, 2010 11:36
por Rodrigo Tomaz » Sex Fev 19, 2010 11:36
Olá, bom dia...
Tenho uma dúvida quanto à idéia final duma questão.
Seu enunciado apenas diz: "Se
a e
b são números reais tais que
![\sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}}=\sqrt[2]{13} \sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}}=\sqrt[2]{13}](/latexrender/pictures/231a482ada01239aeb61a385c37cc927.png)
, quanto vale
![\left|\sqrt[2]{\frac{a}{b}}-\sqrt[2]{\frac{b}{a}} \right| \left|\sqrt[2]{\frac{a}{b}}-\sqrt[2]{\frac{b}{a}} \right|](/latexrender/pictures/f620f4a8e0030886907861db4ec387cd.png)
?"
Então, eu comecei pela primeira expressão jogando a raiz quadrada do valor "13" para o outro lado:
![\left(\sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}} \right)^2=13 \left(\sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}} \right)^2=13](/latexrender/pictures/b53e050df01a58dad78f344a69249aae.png)
Em seguida fui fazendo a resolução comum:
![\left( \sqrt[2]{\frac{a}{b}} \right)^2+2*\sqrt[2]{\frac{a}{b}}*\sqrt[2]{\frac{b}{a}}+\left( \sqrt[2]{\frac{b}{a}} \right)^2=13 \left( \sqrt[2]{\frac{a}{b}} \right)^2+2*\sqrt[2]{\frac{a}{b}}*\sqrt[2]{\frac{b}{a}}+\left( \sqrt[2]{\frac{b}{a}} \right)^2=13](/latexrender/pictures/387f64fa1bfb8eea1300c4068230ac3b.png)

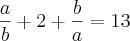

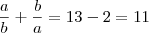
Logo...
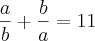
Daí então não consegui complementar a idéia.
Caro professor:
Será que o Senhor pode me ajudar a terminá-la? Ou ainda me dizer se esta idéia não tem fundamento pra achar a resposta em questão?
Agradeço sua atenção e espero resposta.
-
Rodrigo Tomaz
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Fev 19, 2010 10:49
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: técnico mecânica
- Andamento: cursando
 por guijermous » Qui Mar 04, 2010 15:48
por guijermous » Qui Mar 04, 2010 15:48
Boa, tb não consegui resolver. Alguem poderia ajudar?
-
guijermous
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Fev 15, 2010 14:38
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Inf. Industrial
- Andamento: formado
 por MarceloFantini » Qui Mar 04, 2010 22:38
por MarceloFantini » Qui Mar 04, 2010 22:38
Boa noite.
Não tenho certeza da resolução, mas aqui está como eu tentei.
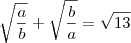
Multiplicando a primeira fração por

em cima e embaixo, e fazendo o mesmo processo na segunda só que multiplicando por

, temos:
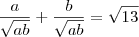

Multiplicando por
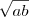
dos dois lados:

Elevando ao quadrado:
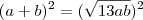
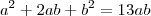
Somando-se

dos dois lados:

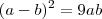
Extraindo a raiz quadrada:

Dividindo-se os dois lados por
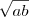
:

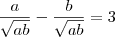
Multiplicando a primeira fração por

em cima e embaixo, e multiplicando a segunda por

do mesmo modo:

Portanto:
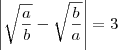
Acredito que seja isso.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Rodrigo Tomaz » Qui Mar 04, 2010 23:16
por Rodrigo Tomaz » Qui Mar 04, 2010 23:16
Boa noite Fantini,
muito obrigado sua resposta está certíssima!
tentei fazer mas achei que a resolução era isolada! mas pelo seu raciocínio vejo que não é tão complicado...
que Deus te abençoe fica na paz vlw!
-
Rodrigo Tomaz
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Fev 19, 2010 10:49
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: técnico mecânica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Modulo
por Sandy26 » Ter Abr 27, 2010 14:46
- 5 Respostas
- 3002 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 17:57
Álgebra Elementar
-
- Módulo
por Bebel » Dom Ago 08, 2010 00:24
- 0 Respostas
- 1380 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:24
Números Complexos
-
- Modulo.
por 380625 » Qui Mar 17, 2011 11:21
- 2 Respostas
- 2095 Exibições
- Última mensagem por LuizAquino

Sex Set 09, 2011 10:47
Cálculo: Limites, Derivadas e Integrais
-
- Módulo
por torilleon » Sáb Ago 20, 2011 19:28
- 2 Respostas
- 1580 Exibições
- Última mensagem por Neperiano

Sáb Ago 20, 2011 20:40
Álgebra Elementar
-
- modulo
por rodrigonapoleao » Seg Jan 21, 2013 13:19
- 1 Respostas
- 1505 Exibições
- Última mensagem por e8group

Seg Jan 21, 2013 15:23
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}}=\sqrt[2]{13} \sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}}=\sqrt[2]{13}](/latexrender/pictures/231a482ada01239aeb61a385c37cc927.png) , quanto vale
, quanto vale ![\left|\sqrt[2]{\frac{a}{b}}-\sqrt[2]{\frac{b}{a}} \right| \left|\sqrt[2]{\frac{a}{b}}-\sqrt[2]{\frac{b}{a}} \right|](/latexrender/pictures/f620f4a8e0030886907861db4ec387cd.png) ?"
?"![\left(\sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}} \right)^2=13 \left(\sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}} \right)^2=13](/latexrender/pictures/b53e050df01a58dad78f344a69249aae.png)
![\left( \sqrt[2]{\frac{a}{b}} \right)^2+2*\sqrt[2]{\frac{a}{b}}*\sqrt[2]{\frac{b}{a}}+\left( \sqrt[2]{\frac{b}{a}} \right)^2=13 \left( \sqrt[2]{\frac{a}{b}} \right)^2+2*\sqrt[2]{\frac{a}{b}}*\sqrt[2]{\frac{b}{a}}+\left( \sqrt[2]{\frac{b}{a}} \right)^2=13](/latexrender/pictures/387f64fa1bfb8eea1300c4068230ac3b.png)

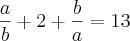

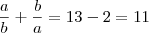
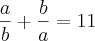



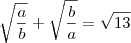
 em cima e embaixo, e fazendo o mesmo processo na segunda só que multiplicando por
em cima e embaixo, e fazendo o mesmo processo na segunda só que multiplicando por  , temos:
, temos: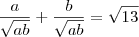

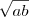 dos dois lados:
dos dois lados:
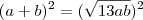
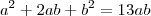
 dos dois lados:
dos dois lados:
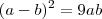


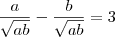

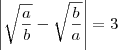



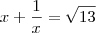
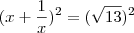
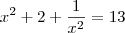
 :
:
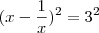
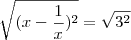

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.