 por rrt » Dom Jul 28, 2013 20:57
por rrt » Dom Jul 28, 2013 20:57
Pessoal, alguém me ajuda a entender a questão abaixo:
CESPE/UnB – SERPRO/2013 - Considerando que x,y e z sejam números naturais tais que
x+y=z;que X seja a proposição “x é ímpar”; que Y seja a proposição
“y é par”; e que Z seja a proposição “z é ímpar”, julgue os seguintes
itens.
A proposição X^Z->Y é verdadeira.
A proposição Y->X^Z é verdadeira.
-
rrt
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Jul 28, 2013 20:42
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MateusL » Dom Jul 28, 2013 23:37
por MateusL » Dom Jul 28, 2013 23:37
A proposição

significa:

é ímpar e

é ímpar implica que

é par.
A proposição
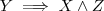
significa:

é par implica que

é ímpar e

é ímpar.
Usando o fato de que

, com
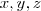
naturais, terás que verificar se essas sentenças são verdadeiras ou falsas.
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Seg Jul 29, 2013 03:47
por Russman » Seg Jul 29, 2013 03:47
Todo número

par pode ser escrito da forma

onde

é um número natural, ao passo de que todo

ímpar pode ser escrito como
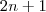
.
Assim, se tomarmos

e

ímpares, então

e

,

e

naturais, de forma que
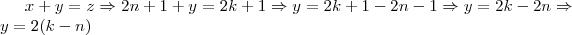
e, garantido que

, então se

e

forem naturais a sua subtração também o é. Logo,

pode ser escrito como

( onde
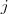
é um número natural) e , portanto,

será par.
Agora, se tomarmos

( um par) , então

A diferença

tem de ser par e isso só ocorre se ambos forem ímpares ou ambos forem pares.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por rrt » Seg Jul 29, 2013 13:37
por rrt » Seg Jul 29, 2013 13:37
Ok, obrigado.
Mas por que a primeira é verdadeira e a segunda é falsa?
A proposição X^Z->Y é verdadeira. Verdadeira
A proposição Y->X^Z é verdadeira. Falsa
-
rrt
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Jul 28, 2013 20:42
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MateusL » Seg Jul 29, 2013 14:52
por MateusL » Seg Jul 29, 2013 14:52
A primeira é verdadeira porque, como o Russman mostrou, se

e

são ímpares, então teremos

par.
Já a segunda sentença é falsa porque, se tivermos

par, não teremos necessariamente

e

ímpares. Como o Russman falou, podemos ter

e

pares. Portanto, sabendo apenas que

é par, não podemos podemos afirmar que

e

são ímpares.
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rrt » Seg Jul 29, 2013 18:32
por rrt » Seg Jul 29, 2013 18:32
Entendi. Obrigado.
-
rrt
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Jul 28, 2013 20:42
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Proposições
por feraferrari » Qui Fev 24, 2011 15:12
- 3 Respostas
- 2718 Exibições
- Última mensagem por LuizAquino

Sex Fev 25, 2011 08:54
Funções
-
- considere as proposiçoes
por flavio neves » Qua Fev 24, 2016 15:10
- 0 Respostas
- 1356 Exibições
- Última mensagem por flavio neves

Qua Fev 24, 2016 15:10
Lógica
-
- Negação das proposições
 por roninhasmr » Seg Nov 13, 2017 14:30
por roninhasmr » Seg Nov 13, 2017 14:30
- 0 Respostas
- 1956 Exibições
- Última mensagem por roninhasmr

Seg Nov 13, 2017 14:30
Lógica
-
- proposições lógicas -torneio
por adrianosaldanha » Qui Out 20, 2011 17:06
- 1 Respostas
- 1818 Exibições
- Última mensagem por fraol

Qua Dez 21, 2011 00:00
Sequências
-
- sistema de proposiçoes e conectivos
por flavio neves » Ter Fev 23, 2016 20:16
- 0 Respostas
- 2403 Exibições
- Última mensagem por flavio neves

Ter Fev 23, 2016 20:16
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 significa:
significa: é ímpar e
é ímpar e  é ímpar implica que
é ímpar implica que  é par.
é par.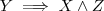 significa:
significa: , com
, com 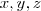 naturais, terás que verificar se essas sentenças são verdadeiras ou falsas.
naturais, terás que verificar se essas sentenças são verdadeiras ou falsas.
 par pode ser escrito da forma
par pode ser escrito da forma  onde
onde  é um número natural, ao passo de que todo
é um número natural, ao passo de que todo 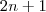 .
. e
e  ,
,  naturais, de forma que
naturais, de forma que 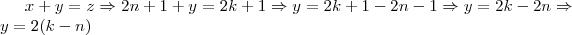
 , então se
, então se  ( onde
( onde 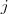 é um número natural) e , portanto,
é um número natural) e , portanto,  ( um par) , então
( um par) , então
 tem de ser par e isso só ocorre se ambos forem ímpares ou ambos forem pares.
tem de ser par e isso só ocorre se ambos forem ímpares ou ambos forem pares.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.