por alineasnovais » Sex Abr 26, 2013 19:04
(X+6)2 = (X-2)2 + (X+5)2
*o 2 fora do parenteses é elevado(desculpe).
pensei que o desenrolar seria assim:
x2 + 36 = x2 +4 + x2 + 25
mas o professor fez assim:
x2 + 12x + 36 = x2 -4x + 4 + x2 + 10x + 25
NÃO ENTENDI! POR FAVOR ME AJUDEM!
-
alineasnovais
-
por DanielFerreira » Sex Abr 26, 2013 21:15
Aline,
seja bem-vinda!
Para resolver essas questões é necessário saber que:
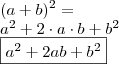
Depois, reduza os termos semelhantes, e, terá uma equação de grau 2. Sabe como resolver uma equação do 2º grau?
Procure apontar onde está a dificuldade, assim poderemos ajudá-la com maior eficácia.
Até breve!
Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação
-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
por alineasnovais » Sex Abr 26, 2013 21:23
Daniel,
Obrigada pelo contato!
Não consigo entender a primeira parte, não entendo o porque do (2.a.b)
para mim seria apenas: (a+b)2 = a2+ b2...
vou colocar em números, eu entendo que o certo é assim: (3+2)2 = 9+4
Obrigada novamente.
-
alineasnovais
-
por DanielFerreira » Sex Abr 26, 2013 21:28
Oi
Aline,
O quadrado do primeiro mais duas vezes o primeiro vezes o segundo mais o quadrado do segundo;
Clique
aqui e leia um pouco!
Caso não entenda, será um prazer ajudá-la!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação
-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
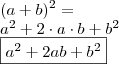
