 por Debylow » Sex Nov 30, 2012 18:32
por Debylow » Sex Nov 30, 2012 18:32
Considere duas funções

e

, definidas por:
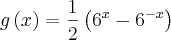
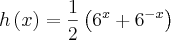
determine o valor da expressão
![\left[h\left(x \right) \right]{}^{2} - \left[g\left(x \right) \right]{}^{2} \left[h\left(x \right) \right]{}^{2} - \left[g\left(x \right) \right]{}^{2}](/latexrender/pictures/9aae39664fccad88048e12b72214fc90.png)
Obg quem puder responder
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por DanielFerreira » Sex Nov 30, 2012 21:29
por DanielFerreira » Sex Nov 30, 2012 21:29
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Debylow » Ter Dez 04, 2012 11:21
por Debylow » Ter Dez 04, 2012 11:21
me explica pq dividiu por 2 e transformou em uma multiplicação ? nao entendi
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por Russman » Ter Dez 04, 2012 20:00
por Russman » Ter Dez 04, 2012 20:00
Existe uma identidade que diz
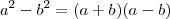
.
Ou seja, a diferença dos quadrados de dois números é igual ao produto da soma pela diferença desses números.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Debylow » Ter Dez 04, 2012 20:41
por Debylow » Ter Dez 04, 2012 20:41
hmm entendi , obg
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Determine o valor de x:]
por Mtfera » Seg Dez 03, 2012 20:58
- 1 Respostas
- 1390 Exibições
- Última mensagem por DanielFerreira

Seg Dez 03, 2012 23:00
Funções
-
- Determine o valor do limite
por Cleyson007 » Sáb Abr 28, 2012 17:27
- 6 Respostas
- 2700 Exibições
- Última mensagem por MarceloFantini

Dom Abr 29, 2012 18:14
Cálculo: Limites, Derivadas e Integrais
-
- determine o valor de x para q se tenha
por weverton » Seg Nov 08, 2010 17:32
- 1 Respostas
- 2544 Exibições
- Última mensagem por davi_11

Qua Nov 24, 2010 13:03
Logaritmos
-
- (Calculo de trigonometria) Determine o valor de x+10
por andersontricordiano » Ter Dez 06, 2011 14:36
- 1 Respostas
- 1557 Exibições
- Última mensagem por MarceloFantini

Ter Dez 06, 2011 14:54
Trigonometria
-
- Determine o valor de L para que a função
por Ana Maria da Silva » Qui Mai 09, 2013 12:11
- 0 Respostas
- 1189 Exibições
- Última mensagem por Ana Maria da Silva

Qui Mai 09, 2013 12:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  , definidas por:
, definidas por: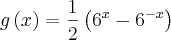
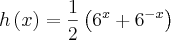
![\left[h\left(x \right) \right]{}^{2} - \left[g\left(x \right) \right]{}^{2} \left[h\left(x \right) \right]{}^{2} - \left[g\left(x \right) \right]{}^{2}](/latexrender/pictures/9aae39664fccad88048e12b72214fc90.png)

 e
e  , definidas por:
, definidas por: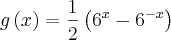
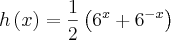
![\left[h\left(x \right) \right]{}^{2} - \left[g\left(x \right) \right]{}^{2} \left[h\left(x \right) \right]{}^{2} - \left[g\left(x \right) \right]{}^{2}](/latexrender/pictures/9aae39664fccad88048e12b72214fc90.png)

![\\ \left [ h(x) \right ]^2 - \left [ g(x) \right ]^2 = \\\\ \left [ h(x) + g(x) \right ]\left [ h(x) - g(x) \right ] = \\\\\\ \left [ \frac{6^x + 6^{- x}}{2} + \frac{6^x - 6^{- x}}{2} \right ]\left [ \frac{6^x + 6^{- x}}{2} - \frac{6^x - 6^{- x}}{2} \right ] = \\\\\\ \left [ \frac{6^x + \cancel{6^{- x}} + 6^x \cancel{- 6^{- x}}}{2} \right ]\left [ \frac{\cancel{6^x} + 6^{- x} \cancel{- 6^x} + 6^{- x}}{2} \right ] = \\\\\\ \left ( \frac{2 \cdot 6^x}{2} \right ) \left ( \frac{2 \cdot 6^{- x}}{2} \right ) = \\\\\\ 6^x \cdot 6^{- x} = \\\\ 6^{x - x} = \\\\ 6^0 = \\\\ \boxed{1} \\ \left [ h(x) \right ]^2 - \left [ g(x) \right ]^2 = \\\\ \left [ h(x) + g(x) \right ]\left [ h(x) - g(x) \right ] = \\\\\\ \left [ \frac{6^x + 6^{- x}}{2} + \frac{6^x - 6^{- x}}{2} \right ]\left [ \frac{6^x + 6^{- x}}{2} - \frac{6^x - 6^{- x}}{2} \right ] = \\\\\\ \left [ \frac{6^x + \cancel{6^{- x}} + 6^x \cancel{- 6^{- x}}}{2} \right ]\left [ \frac{\cancel{6^x} + 6^{- x} \cancel{- 6^x} + 6^{- x}}{2} \right ] = \\\\\\ \left ( \frac{2 \cdot 6^x}{2} \right ) \left ( \frac{2 \cdot 6^{- x}}{2} \right ) = \\\\\\ 6^x \cdot 6^{- x} = \\\\ 6^{x - x} = \\\\ 6^0 = \\\\ \boxed{1}](/latexrender/pictures/a109ef10d1b60811eff51d63f6db8b40.png)


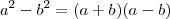 .
.


 .
.
 :
: