Você acertou as funções elementares envolvidas. Mais precisamente,

.
Agora, quais são as operações usuais de funções? Soma, subtração, multiplicação, divisão (quando a divisora é diferente de zero) e composição. Se denominarmos
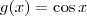
e
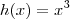
.
Vejamos as expressões de cada uma:
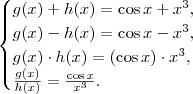
Ora, nenhuma destas expressões correspondem à função dada. Por eliminação, só pode ser composição.
O que eu acabei de fazer foi a maneira grosseira de descobrir quando é composição (neste caso simples).
Para enxergar a composição, pense no seguinte: quando escrevemos
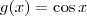
, sabemos que

é um número (real, usualmente), correto? Então qualquer número dentro do domínio, claro, pode ser colocado lá. Além disso, a variável é 'muda', ou seja,

é o mesmo que
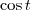
,
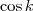
,
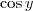
,

,

, e assim em diante (assumindo que estas variáveis não denotem outra coisa).
Portanto, se podemos colocar qualquer número, quero colocar em particular o número igual a
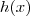
. Assim como avaliamos funções no domínio, como
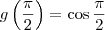
, posso avaliá-la no ponto
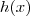
, escrevendo
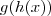
, que tem valor

.
Mas nós temos uma expressão para
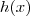
, que é justamente

. Substituindo segue que

. É isto que quero dizer quando uma função está "dentro" da outra. No lugar da variável usual, a variável torna-se uma nova função.
![y=\sqrt[]{x}.sen x y=\sqrt[]{x}.sen x](/latexrender/pictures/9d865190c07c423023adbdaf5fb93af0.png)



 temos que
temos que  é real, logo isso inclui
é real, logo isso inclui  ,
,  ,
, 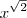 ,
,  , etc.
, etc.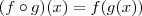 . Vamos tomar o caso
. Vamos tomar o caso  e
e  . Então
. Então 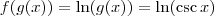 .
. ,
, 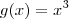 e
e  . Encontre
. Encontre  . Pela definição dada, isto é
. Pela definição dada, isto é  .
.

 e
e  são duas funções elementares. Uma parece estar "dentro" da outra? Quando eu digo "dentro", quero dizer que a variável da função é algo diferente de
são duas funções elementares. Uma parece estar "dentro" da outra? Quando eu digo "dentro", quero dizer que a variável da função é algo diferente de  , mais precisamente é uma outra função de
, mais precisamente é uma outra função de  .
. e
e  , logo
, logo  .
. . Quais são as funções elementares envolvidas?
. Quais são as funções elementares envolvidas?
 .
.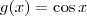 e
e 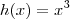 .
.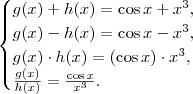
 é o mesmo que
é o mesmo que 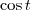 ,
, 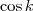 ,
, 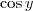 ,
,  ,
,  , e assim em diante (assumindo que estas variáveis não denotem outra coisa).
, e assim em diante (assumindo que estas variáveis não denotem outra coisa).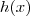 . Assim como avaliamos funções no domínio, como
. Assim como avaliamos funções no domínio, como 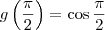 , posso avaliá-la no ponto
, posso avaliá-la no ponto 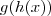 , que tem valor
, que tem valor  .
. . Substituindo segue que
. Substituindo segue que  . É isto que quero dizer quando uma função está "dentro" da outra. No lugar da variável usual, a variável torna-se uma nova função.
. É isto que quero dizer quando uma função está "dentro" da outra. No lugar da variável usual, a variável torna-se uma nova função.![y=\sqrt[]{2x+1} y=\sqrt[]{2x+1}](/latexrender/pictures/7692140ab9009acb94457536be429c46.png) (Aproveitando porque esta função é composta??)
(Aproveitando porque esta função é composta??)
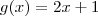 e
e  , assim
, assim  .
.  e
e 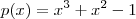 . Então
. Então 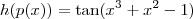 .
.



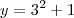
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.
