 por thayna_rosa » Seg Nov 12, 2012 18:46
por thayna_rosa » Seg Nov 12, 2012 18:46
Determine as coordenadas do vértice da parábola que representa a função: g(x)=-3(x-4)²+2
-
thayna_rosa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Nov 12, 2012 18:28
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por thayna_rosa » Seg Nov 12, 2012 20:01
por thayna_rosa » Seg Nov 12, 2012 20:01
não sei o que fazer depois que resolvo o produto notável
-
thayna_rosa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Nov 12, 2012 18:28
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Seg Nov 12, 2012 20:47
por MarceloFantini » Seg Nov 12, 2012 20:47
Existem duas formas de responder: uma é lembrar que a abscissa do vértice é dada por
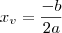
, substituir na fórmula e encontrar a ordenada

correspondente.
Outra forma, mais interessante, é perceber que
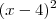
sempre será maior ou igual a zero, pois é um número ao quadrado. Daí temos que
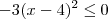
pelas propriedades de desigualdade. Somando-se dois de ambos lados segue que
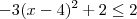
. Isto acontece se e somente se

, que é a condição para que
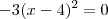
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9225 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2632 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2012 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2090 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 8038 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




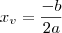 , substituir na fórmula e encontrar a ordenada
, substituir na fórmula e encontrar a ordenada  correspondente.
correspondente.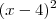 sempre será maior ou igual a zero, pois é um número ao quadrado. Daí temos que
sempre será maior ou igual a zero, pois é um número ao quadrado. Daí temos que 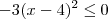 pelas propriedades de desigualdade. Somando-se dois de ambos lados segue que
pelas propriedades de desigualdade. Somando-se dois de ambos lados segue que 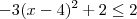 . Isto acontece se e somente se
. Isto acontece se e somente se  , que é a condição para que
, que é a condição para que 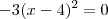 .
.

