 por Mariana Martin » Ter Set 11, 2012 18:20
por Mariana Martin » Ter Set 11, 2012 18:20
Oi, pessoal!
Simplificando a expressão:
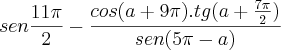
, obtém-se:
Resposta:
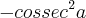
Minha resolução foi:
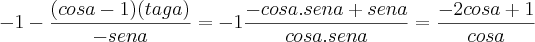
Como vocês podem ver, o resultado não bateu... Me ajudem, por favor, a achar meu erro. Já repeti esse exercício várias vezes, e nada.
Obrigada
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Ter Set 11, 2012 19:34
por young_jedi » Ter Set 11, 2012 19:34
Oi Mariana Martin
sugiro que para esta questão vc utilize as identidade trigonometircas
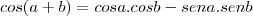
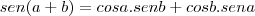
assim tera
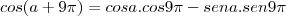
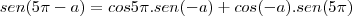
resolvendo
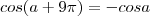
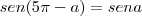
para
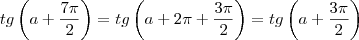
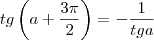
sua equação ficaria então
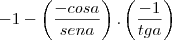
apartir dai da pra chegar a resposta
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Mariana Martin » Qua Set 12, 2012 21:37
por Mariana Martin » Qua Set 12, 2012 21:37
Não entendi essa parte:
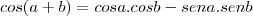
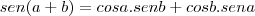
Cada uma é uma identidade ou é continuação?
Me desculpe, mas nunca tinha vista essa identidade imaginei que era preciso apenas fazer distributiva. assim:
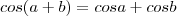
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Qua Set 12, 2012 21:43
por Cleyson007 » Qua Set 12, 2012 21:43
Mariana, boa noite!
Desculpe tomar a liberdade de responder a sua dúvida (faço-o devido o nosso amigo young_jed não estar online no momento).
São identidadades trigonométricas!
--> Cada caso é um caso (uma é para o seno e a outra para o cosseno).
Comente qualquer dúvida

Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Mariana Martin » Sáb Set 15, 2012 09:30
por Mariana Martin » Sáb Set 15, 2012 09:30
Entendi.
Estava lendo num livro didático a seguinte identidade trigonométrica:
cos(p-a) = -cosa
só que há essa também:
cos(p-a) = cosp.cosa - senp.sena
Como pode haver duas identidades para o mesmo caso?
Obrigada
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sáb Set 15, 2012 11:08
por DanielFerreira » Sáb Set 15, 2012 11:08
Olá
Mariana,
bom dia!
O correto é:
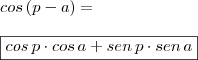
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Sáb Set 15, 2012 12:30
por MarceloFantini » Sáb Set 15, 2012 12:30
A menos que esse tal

seja

. Isto pode ser verificado usando a identidade dada:
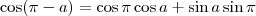
, mas
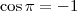
e
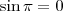
, daí
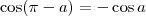
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Mariana Martin » Seg Set 24, 2012 09:43
por Mariana Martin » Seg Set 24, 2012 09:43
Entendi. Obrigada pela ajuda pessoal!
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Mariana Martin » Seg Set 24, 2012 11:52
por Mariana Martin » Seg Set 24, 2012 11:52
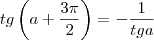
Desculpe pessoal, estava revendo este trecho e não entendi porque dá esse resultado.
Porque Tg(a+b) = tga + tgb / 1 - tga.tab
E não bate o resultado segundo essa identidade
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Seg Set 24, 2012 14:37
por young_jedi » Seg Set 24, 2012 14:37
se voce utlizar essa relação voce tera que
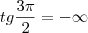
então não da para utilizar essa relação para esse caso
por isso vc tem que fazer uma analise do circulo trigonometrico para chegar ao valor correto
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Mariana Martin » Seg Set 24, 2012 15:35
por Mariana Martin » Seg Set 24, 2012 15:35
Como?
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções circulares
 por Mariana Martin » Seg Set 24, 2012 15:20
por Mariana Martin » Seg Set 24, 2012 15:20
- 1 Respostas
- 1413 Exibições
- Última mensagem por young_jedi

Seg Set 24, 2012 15:52
Trigonometria
-
- Funções circulares inversas
por Ananda » Qui Mar 20, 2008 20:03
- 2 Respostas
- 4803 Exibições
- Última mensagem por Ananda

Seg Mar 24, 2008 17:13
Trigonometria
-
- funçoes circulares inversas
por Thassya » Sex Mai 29, 2009 11:29
- 3 Respostas
- 2524 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 10:18
Trigonometria
-
- Função Circulares inversas 2
por Fernanda90 » Qui Ago 27, 2009 16:52
- 2 Respostas
- 4223 Exibições
- Última mensagem por Fernanda90

Qui Ago 27, 2009 20:25
Trigonometria
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3428 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
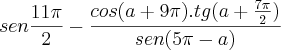 , obtém-se:
, obtém-se: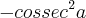
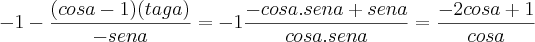

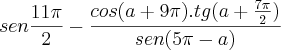 , obtém-se:
, obtém-se: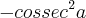
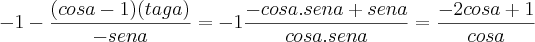

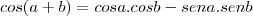
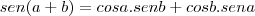
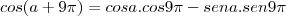
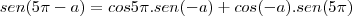
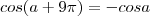
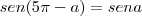
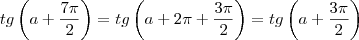
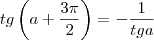
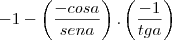

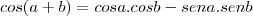
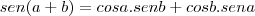
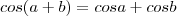




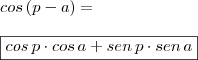

 seja
seja  . Isto pode ser verificado usando a identidade dada:
. Isto pode ser verificado usando a identidade dada: 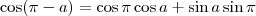 , mas
, mas 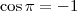 e
e 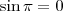 , daí
, daí 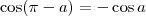 .
.


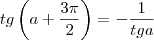

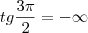



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.