Não, isto não está correto. Não existe igualar bases, veja que em

não há sentido em "igualar as bases". O que você diz é sim quando temos exponenciais de
mesma base, não que igualamos. Neste caso, para que sejam iguais, deve-se ocorrer que os expoentes são os mesmos devido ao fato que a função exponencial é injetora.
Esta questão é uma das tradicionais mudanças de variável. É importante lembrar a propriedade fundamental da função exponencial de que ela
nunca se anula, ou seja,
 SEMPRE
SEMPRE, para todo

. Perceba que
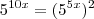
. Então faça
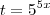
. A equação toma a forma
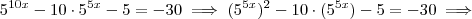

.
Temos agora uma equação do segundo grau em t. Tente prosseguir e mostre seus passos.
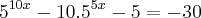
 , se não me engano. E no caso a expressão fica:
, se não me engano. E no caso a expressão fica: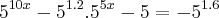


 não há sentido em "igualar as bases". O que você diz é sim quando temos exponenciais de
não há sentido em "igualar as bases". O que você diz é sim quando temos exponenciais de 
 . Perceba que
. Perceba que 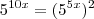 . Então faça
. Então faça 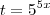 . A equação toma a forma
. A equação toma a forma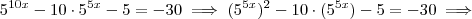
 .
.


 , certo? Mas lá no começo dissemos que
, certo? Mas lá no começo dissemos que  , daí
, daí 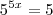 e
e  , logo
, logo  .
.