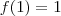por nathyn » Ter Nov 29, 2011 18:39
por nathyn » Ter Nov 29, 2011 18:39
Olá, se alguem puder me ajudar por favor...
eu gostaria de saber o que significa um ponto fixo em função, exemplo:
Sendo y = f(x) uma função real, se f(x) = x para algum x, dizemos que x é um ponto fico de f.
O que ele quis dizer? O que é ponto fixo?
Agradeço a quem puder ajudar -)
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por TheoFerraz » Ter Nov 29, 2011 18:58
por TheoFerraz » Ter Nov 29, 2011 18:58
nathyn escreveu:Sendo y = f(x) uma função real, se f(x) = x para algum x, dizemos que x é um ponto fico de f.
justamente o que está escrito!
observe... se para algum

tivermos a seguinte situação
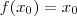
entao vamos chamar

de pto fixo...
vou dar um exemplo:

mostre ptos fixos...
bom, pela definição
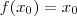
entao

pois a função é

chegamos na expressão

que pode ser fatorada da forma
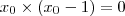
para tanto

ou

esses são os ptos fixos da função pois observe:
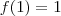
e

deu pra pegar ?
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por MarceloFantini » Ter Nov 29, 2011 19:14
por MarceloFantini » Ter Nov 29, 2011 19:14
Pense assim: algo que está fixo tem a propriedade que não se altera, ou seja, não troca de lugar, não sofre mudanças. Com esse contexto, um ponto fixo de uma função é um ponto que não sai do lugar quando aplicamos a função.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nathyn » Ter Nov 29, 2011 21:29
por nathyn » Ter Nov 29, 2011 21:29
Aaah siim... Entendii
Deu pra pegar muitoo Theo, brigadão .D
Brigada Marcelo tbm, "algo que não se altera",=)
Brigadão gente...
Fiquem com Deus
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema ponto fixo (Livro do Thomas Ed Pearson)
por Luiz Augusto Prado » Ter Dez 22, 2009 16:02
- 2 Respostas
- 2415 Exibições
- Última mensagem por Luiz Augusto Prado

Qua Dez 23, 2009 15:07
Funções
-
- Três pontos definem quantas esferas com raio fixo?
por yuriprovase » Sáb Jun 25, 2016 01:09
- 1 Respostas
- 7805 Exibições
- Última mensagem por e8group

Sáb Jun 25, 2016 21:18
Geometria Espacial
-
- ponto da reta r que é eqüidistante do ponto A e do ponto B
por gutorocher » Qua Jul 21, 2010 14:01
- 12 Respostas
- 15142 Exibições
- Última mensagem por gutorocher

Sex Jul 23, 2010 13:04
Geometria Analítica
-
- [Vetores] Ponto de reta próximo a outros pares de ponto
por cmcrz97 » Ter Jun 19, 2018 20:29
- 0 Respostas
- 2906 Exibições
- Última mensagem por cmcrz97

Ter Jun 19, 2018 20:29
Álgebra Linear
-
- [Ponto Crítico e Ponto de Inflexão e intervalos] Dúvidas em
por Andre Lopes » Qua Set 26, 2012 00:37
- 2 Respostas
- 3370 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 06:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 tivermos a seguinte situação
tivermos a seguinte situação 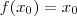 entao vamos chamar
entao vamos chamar 
 pois a função é
pois a função é 
 que pode ser fatorada da forma
que pode ser fatorada da forma 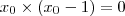
 ou
ou