 por jcvalim » Qua Ago 24, 2011 11:39
por jcvalim » Qua Ago 24, 2011 11:39
Considere a função real f definida por

, sendo g de A a sua inversa. Considere também as seguintes afirmativas. Verifique as falsas e as verdadeiras, justificando sua resposta.
a) a imagem de f é A.
b) o gráfico de f está acima da reta y = 4
c)
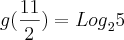
d) Se f (h(x)) = 3 + 2x então h(¼) = 0
e) O gráfico da função g intercepta o eixo x no ponto (1,0)
f) O conjunto solução da inequação
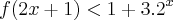
é o intervalo ]0,1[
Se faz necessario as soluções de cada resposta.
A primeira eu fiz e sei que é Falsa pois A não pode ser imagem de f, pois se A é a função então A é o dominio então a imagem será B.

Obrigado, a todos!!!
-
jcvalim
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 24, 2011 11:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Qua Ago 24, 2011 13:47
por MarceloFantini » Qua Ago 24, 2011 13:47
Note que o maior domínio possível de f é

, enquanto que sua imagem é

. Portanto, sua inversa será definida:
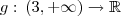
, portanto a primeira é falsa. Seu argumento não é válido pois é possível ter uma função com domínio e imagem iguais. Vamos encontrar a função inversa:
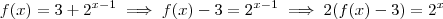

Verifique as afirmações. A letra b é falsa, pois tome

, temos
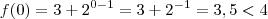
e portanto o gráfico de f não está acima da reta y=4 (existem outros pontos, foi para ilustrar, mesmo porque o conjunto imagem demonstra que há infinitos pontos abaixo da reta).
Tente fazer as outras letras.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jcvalim » Qua Ago 24, 2011 16:48
por jcvalim » Qua Ago 24, 2011 16:48
Mas no caso da letra B se eu tomasse o X=2, eu poderia utilizar o X sendo < que 2?
-
jcvalim
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 24, 2011 11:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Qua Ago 24, 2011 16:50
por MarceloFantini » Qua Ago 24, 2011 16:50
Note que

não é contra-exemplo, uma vez que
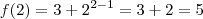
e está acima da reta

. Mesmo tomando

, o seu exemplo não garante que existam pontos do gráfico abaixo da reta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jcvalim » Qua Ago 24, 2011 17:26
por jcvalim » Qua Ago 24, 2011 17:26
MarceloFantini escreveu:Note que

não é contra-exemplo, uma vez que
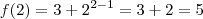
e está acima da reta

. Mesmo tomando

, o seu exemplo não garante que existam pontos do gráfico abaixo da reta.
Entendi agora.
Só mais uma coisa poderia me dar um auxilio com essa questão que envolve o logaritmo, pois estou travado nela. As outras da para desenrolar. A letra C
Obrigado!!!
-
jcvalim
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 24, 2011 11:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Qua Ago 24, 2011 17:48
por MarceloFantini » Qua Ago 24, 2011 17:48
Você tentou substituir

e ver se o valor é igual ao afirmado na letra C?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jcvalim » Qua Ago 24, 2011 18:03
por jcvalim » Qua Ago 24, 2011 18:03
MarceloFantini escreveu:Você tentou substituir

e ver se o valor é igual ao afirmado na letra C?
Então mas a função e f(x) e na afirmação ele esta utilizando g(x).
-
jcvalim
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 24, 2011 11:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Qua Ago 24, 2011 18:09
por MarceloFantini » Qua Ago 24, 2011 18:09
Eu já te dei a expressão para a inversa, investigue o outro post.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real de variável real!
por kellykcl » Qui Mai 01, 2014 13:41
- 2 Respostas
- 3267 Exibições
- Última mensagem por kellykcl

Qui Mai 01, 2014 16:28
Funções
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5571 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [Desafio: função real]Determinar a função f(x)
por raimundosar » Qui Mai 05, 2016 19:02
- 1 Respostas
- 2460 Exibições
- Última mensagem por nakagumahissao

Sex Mai 06, 2016 00:25
Funções
-
- função real
por cristina » Seg Abr 19, 2010 23:54
- 2 Respostas
- 2162 Exibições
- Última mensagem por MarceloFantini

Ter Abr 20, 2010 19:43
Funções
-
- Função Real..
por Leone de Paula » Sáb Jul 17, 2010 15:39
- 1 Respostas
- 1698 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 16:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , sendo g de A a sua inversa. Considere também as seguintes afirmativas. Verifique as falsas e as verdadeiras, justificando sua resposta.
, sendo g de A a sua inversa. Considere também as seguintes afirmativas. Verifique as falsas e as verdadeiras, justificando sua resposta.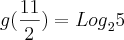
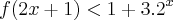 é o intervalo ]0,1[
é o intervalo ]0,1[


 , enquanto que sua imagem é
, enquanto que sua imagem é  . Portanto, sua inversa será definida:
. Portanto, sua inversa será definida: 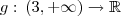 , portanto a primeira é falsa. Seu argumento não é válido pois é possível ter uma função com domínio e imagem iguais. Vamos encontrar a função inversa:
, portanto a primeira é falsa. Seu argumento não é válido pois é possível ter uma função com domínio e imagem iguais. Vamos encontrar a função inversa: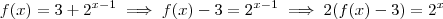

 , temos
, temos 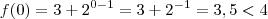 e portanto o gráfico de f não está acima da reta y=4 (existem outros pontos, foi para ilustrar, mesmo porque o conjunto imagem demonstra que há infinitos pontos abaixo da reta).
e portanto o gráfico de f não está acima da reta y=4 (existem outros pontos, foi para ilustrar, mesmo porque o conjunto imagem demonstra que há infinitos pontos abaixo da reta).

 não é contra-exemplo, uma vez que
não é contra-exemplo, uma vez que 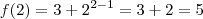 e está acima da reta
e está acima da reta  . Mesmo tomando
. Mesmo tomando  , o seu exemplo não garante que existam pontos do gráfico abaixo da reta.
, o seu exemplo não garante que existam pontos do gráfico abaixo da reta. e ver se o valor é igual ao afirmado na letra C?
e ver se o valor é igual ao afirmado na letra C?