 por OtavioBonassi » Qui Jul 14, 2011 23:04
por OtavioBonassi » Qui Jul 14, 2011 23:04
Galera, tenho um sério caô em trabalhar com função inversa de polinomios ,como eu resolvo "Função inversa de x³ + 2x + 1"
Na verdade o exercício é o seguinte :
"Se f(x) = x³ + 2x + 1 e g é a função inversa de f, entao g'(1) é igual a :"
Não sei se tem alguma relaçao entre os dois coeficientes de funçoes inversas, tem ?
Valeu !
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Molina » Sex Jul 15, 2011 12:22
por Molina » Sex Jul 15, 2011 12:22
Bom dia, Otavio.
De que livro você retirou esta questão? Pergunto isso pois a inversa dessa função é um tanto quanto complexa, como você pode ver
clicando aqui.
Mas podemos perceber que a f intercepta o eixo y no ponto 1:
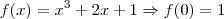
Como a inversa é simétrica em relação a y = x, temos que a g vai interceptar o eixo x no ponto 1.
Ou seja,


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Sex Jul 15, 2011 20:08
por MarceloFantini » Sex Jul 15, 2011 20:08
Imagino que a questão seja sobre Cálculo 1, visto que pelo o que eu li ele quer
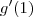
e não

. Basta aplicar o teorema da derivada da função inversa (que eu não me lembro agora).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Jul 15, 2011 21:51
por LuizAquino » Sex Jul 15, 2011 21:51
Note que
não é necessário determinar explicitamente a expressão da função g.
Queremos apenas calcular g'(1).
Como sugeriu Fantini, utilizando o teorema da derivada da função inversa, sabemos que
![[f^{-1}(x)]^\prime = \frac{1}{f^\prime\left(f^{-1}(x)\right)} [f^{-1}(x)]^\prime = \frac{1}{f^\prime\left(f^{-1}(x)\right)}](/latexrender/pictures/d24cfca99a4cda57b8781f7078c57941.png)
.
Portanto, nesse exercício temos que
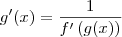
.
Isso significa que

.
Note que todo o seu trabalho irá se resumir a determinar a derivada de
f e calculá-la em
g(1). Em seguida, basta tomar o inverso desse número.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Molina » Sex Jul 15, 2011 22:11
por Molina » Sex Jul 15, 2011 22:11
Boa noite.
Peço desculpas por não ter visto o símbolo de derivada na função g.

Bom final de semana a todos!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por OtavioBonassi » Sáb Jul 16, 2011 12:38
por OtavioBonassi » Sáb Jul 16, 2011 12:38
Opa, desconhecia esse teorema da função inversa, acho que isso facilita bastante a resolução hehe.
Valeu !
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por LuizAquino » Sáb Jul 16, 2011 18:14
por LuizAquino » Sáb Jul 16, 2011 18:14
OtavioBonassi escreveu:Opa, desconhecia esse teorema da função inversa, acho que isso facilita bastante a resolução hehe.
Se você desejar estudar mais sobre a derivada de funções inversas, então assista a
vídeo-aula "15. Cálculo I - Derivada da Função Inversa". Eu acredito que ela possa lhe ajudar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função inversa
por gisa123 » Qui Ago 28, 2008 17:22
- 1 Respostas
- 3397 Exibições
- Última mensagem por Molina

Qui Ago 28, 2008 23:53
Funções
-
- O que é função inversa
por irineu junior » Sex Mar 12, 2010 20:57
- 2 Respostas
- 2642 Exibições
- Última mensagem por irineu junior

Dom Mar 14, 2010 16:28
Funções
-
- Função Inversa.
por jcvalim » Qua Ago 24, 2011 15:57
- 0 Respostas
- 1185 Exibições
- Última mensagem por jcvalim

Qua Ago 24, 2011 15:57
Funções
-
- função inversa
por tigre matematico » Qui Out 13, 2011 12:45
- 1 Respostas
- 2209 Exibições
- Última mensagem por Guill

Sáb Abr 21, 2012 18:07
Funções
-
- Função Inversa
por Rafael16 » Qua Mar 14, 2012 12:08
- 3 Respostas
- 1971 Exibições
- Última mensagem por LuizAquino

Qua Mar 14, 2012 15:16
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


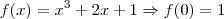



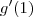 e não
e não  . Basta aplicar o teorema da derivada da função inversa (que eu não me lembro agora).
. Basta aplicar o teorema da derivada da função inversa (que eu não me lembro agora).
![[f^{-1}(x)]^\prime = \frac{1}{f^\prime\left(f^{-1}(x)\right)} [f^{-1}(x)]^\prime = \frac{1}{f^\prime\left(f^{-1}(x)\right)}](/latexrender/pictures/d24cfca99a4cda57b8781f7078c57941.png) .
.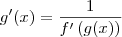 .
. .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

