 por davi1993 » Seg Jun 20, 2011 12:51
por davi1993 » Seg Jun 20, 2011 12:51
galera é o seguinte: tenho prova hoje de calculo, dai nos meus estudos aqui, intalei nesse exercicio de funcao do segundo grau abaixo
se alguem puder me ajudar, explicando a resolucao seria de grande ajuda.. nao consigo de maneira alguma encaixar esse "-100 unidades por mes" na funcao =\
elevei tudo ao quadrado tentei tirar as raizes, mas nada... nao chego numa funcao do segundo grau nem ferrando
o exercicio é:
" Uma fábrica de móveis produz um modelo especial de cama. Após a procura de um modelo matemático para estimar sua produção, chegou-se a conclusão que a quantidade mensal produzida tem sindo aproximadamente cinquenta vezes a raiz quadrada do número de funcionários. Por causa de uma queda nas vendas, a empresa dispensou 48 funcionários e, com isso, passou a produzir 100 unidades a menos por mês. Quantos eram os funcionários antes da dispensa? "tentei de tudo, f(x) = (50*raiz(x-48))-100
mas naada =\
se puderem me ajudar... obrigado

-
davi1993
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jun 20, 2011 12:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: sistemas de informacao
- Andamento: cursando
 por Molina » Seg Jun 20, 2011 14:01
por Molina » Seg Jun 20, 2011 14:01
Boa tarde.
Seja
f(x) o número de móveis produzidos e
x o número de funcionários. Assim:
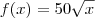
Com a queda de funcionários, houve também queda de produção:

Igualando as duas equações:
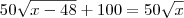
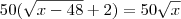
 Desenvolvendo isso...
Desenvolvendo isso...
Ou seja, este era o número de funcionários antes da dispensa.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por davi1993 » Seg Jun 20, 2011 14:29
por davi1993 » Seg Jun 20, 2011 14:29
Boa tarde!
Molina, muito obrigado pela ajudaa =D
estava com dificuldade em encaixar o 100
segui os passos, e cheguei na seguinte equacao
raiz(x-48)+2 = raiz(x)
se nao for pedir demais, teria como me ajudar novamente no desenvolvimento dessa equacao ?
tentei elevar ambos os lados ao quadrado
mas nao chego no 169
elevando os 2 lados ao quadrado eu teria, x-48+4 = x certo?
nao consigo ir à lugar algum =\
obrigado
-
davi1993
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jun 20, 2011 12:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: sistemas de informacao
- Andamento: cursando
 por Molina » Seg Jun 20, 2011 14:37
por Molina » Seg Jun 20, 2011 14:37
Boa tarde.
davi1993 escreveu:Boa tarde!
Molina, muito obrigado pela ajudaa =D
estava com dificuldade em encaixar o 100
segui os passos, e cheguei na seguinte equacao
raiz(x-48)+2 = raiz(x)
se nao for pedir demais, teria como me ajudar novamente no desenvolvimento dessa equacao ?
tentei elevar ambos os lados ao quadrado
mas nao chego no 169
elevando os 2 lados ao quadrado eu teria, x-48+4 = x certo?
nao consigo ir à lugar algum =\
obrigado
Na verdade não é desta forma não, lembre-se de produtos notáveis:

Eu estou sem tempo de resolver agora. Estarei disponível após as 17h. Se for útil ainda eu te ajudo...
Mas tente fazer o seguinte:


Agora eleve os dois lados ao quadrado. Provavelmente você ficará com raiz ainda, então faça novamente o procedimento até conseguir retirar esta raiz. Caso não consiga, avise que após as 17h eu te ajudo.
Bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por davi1993 » Seg Jun 20, 2011 15:52
por davi1993 » Seg Jun 20, 2011 15:52
realmente, eu estava pecando nos produtos notáveis
vlww pela ajuda novamente

conseguir resolver =p
obrigado!
-
davi1993
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jun 20, 2011 12:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: sistemas de informacao
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguem poderia me ajudar com esse exercicio ?
por rodrigo321 » Dom Dez 06, 2009 03:33
- 1 Respostas
- 2016 Exibições
- Última mensagem por Molina

Dom Dez 06, 2009 12:09
Cálculo: Limites, Derivadas e Integrais
-
- Dúvidas em Pa, alguém poderia me ajudar?
por plugpc » Qui Out 01, 2009 18:22
- 2 Respostas
- 1906 Exibições
- Última mensagem por DanielFerreira

Sex Out 02, 2009 01:08
Álgebra Elementar
-
- (geometria plana)Alguém poderia me ajudar.
por Thainara » Qui Mai 19, 2016 12:08
- 2 Respostas
- 7125 Exibições
- Última mensagem por Thainara

Qui Mai 19, 2016 15:27
Geometria Plana
-
- Alguém poderia me ajudar a responder esses exercícios.?
por icarowilliams15 » Seg Jun 13, 2011 12:12
- 7 Respostas
- 4327 Exibições
- Última mensagem por icarowilliams15

Qua Jun 15, 2011 10:57
Funções
-
- Alguem poderia resolver esse exercicio
por Justiceira » Sex Dez 04, 2009 22:00
- 1 Respostas
- 2681 Exibições
- Última mensagem por Molina

Sex Dez 04, 2009 22:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



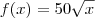

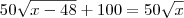
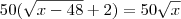







 , avisa que eu resolvo.
, avisa que eu resolvo.

