 não-constante e tal que
não-constante e tal que 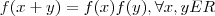 . Das afirmações :
. Das afirmações :I)
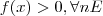 naturais não-nulos
naturais não-nulosII)
![f(nx)= {[f(x)]}^{n}, \forall x E f(nx)= {[f(x)]}^{n}, \forall x E](/latexrender/pictures/c08b8d884ee44470260ef2f39dcd656a.png) Reais,
Reais,  naturais não-nulos
naturais não-nulosIII)
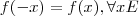 Reais.
Reais.
 não-constante e tal que
não-constante e tal que 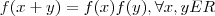 . Das afirmações :
. Das afirmações :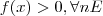 naturais não-nulos
naturais não-nulos![f(nx)= {[f(x)]}^{n}, \forall x E f(nx)= {[f(x)]}^{n}, \forall x E](/latexrender/pictures/c08b8d884ee44470260ef2f39dcd656a.png) Reais,
Reais,  naturais não-nulos
naturais não-nulos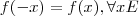 Reais.
Reais.


 . Ou seja, a função terá valor a independente do x escolhido. Exemplos:
. Ou seja, a função terá valor a independente do x escolhido. Exemplos: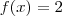


 , porém não há n na função. [Esclareça se não há algum erro de digitação]
, porém não há n na função. [Esclareça se não há algum erro de digitação] 
![f(nx)=f(x + x + ... + x)=f(x)*f(x)*...*f(x)=[f(x)]^n \Rightarrow f(nx)=[f(x)]^n f(nx)=f(x + x + ... + x)=f(x)*f(x)*...*f(x)=[f(x)]^n \Rightarrow f(nx)=[f(x)]^n](/latexrender/pictures/d657a1c42edeb21a914f66fffaaec564.png)



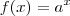 ,mas não é necessário saber disso para resolver a questão.Ja vou assumir a prova do molina do segundo e provar que o terceiro é falso, para poder provar o primeiro.
,mas não é necessário saber disso para resolver a questão.Ja vou assumir a prova do molina do segundo e provar que o terceiro é falso, para poder provar o primeiro.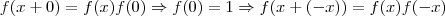

 .Como
.Como 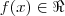 então
então  e como f(x) é diferente de 0 ,temos:
e como f(x) é diferente de 0 ,temos: e como isto é valido para todo x real então se x=y/2 tambem vai ser valido para todo y real,logo
e como isto é valido para todo x real então se x=y/2 tambem vai ser valido para todo y real,logo  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)