 por plugpc » Ter Ago 18, 2009 19:54
por plugpc » Ter Ago 18, 2009 19:54
Numa PA com números ímpar de termos, a soma dos termos de ordem ímpar é 63 e a dos termos de ordem par é 54. Achar n.
R- 13
Gostaria da ajuda de vocês para sanar minhas dúvidas já usei várias fórmulas mas nenhuma chega ao resultado correto pois é a primeira vez que resolvo esse tipo de questão...Se não for abusar da boa vontade de vocês me expliquem pois desde já fico grato
Plugpc...
-
plugpc
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Jul 07, 2008 22:00
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matemática
- Andamento: cursando
 por Lucio Carvalho » Qua Ago 19, 2009 12:51
por Lucio Carvalho » Qua Ago 19, 2009 12:51
Olá plugpc,
Sabemos que para calcular a soma dos n primeiros termos de uma progressão aritmética usamos a fórmula:
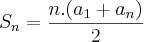
.
Agora, se dizes que a PA tem número de termos ímpar, a soma dos termos de ordem ímpar é 63 e a dos termos de ordem par é 54, então podemos concluir que:
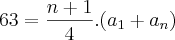
e
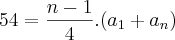
Isto quer dizer que:
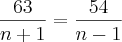
Resolvendo em ordem a n, teremos:

Bye bye e espero ter ajudado!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


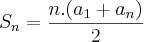 .
.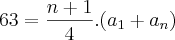 e
e 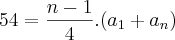
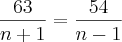


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.