 por fenixxx » Seg Ago 13, 2012 14:01
por fenixxx » Seg Ago 13, 2012 14:01
Estou tentando entender indução matematica, mas travei também nessa questão de indução Forte, alguem pode me ajudar ?
Seja a sequência a1, a2, a3, . . . definida como:
a1 = 1, a2 = 3
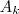
=
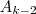
+

para todos inteiros k >=3
Mostre usando Indução Forte que
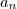
é ?mpar para todo n natural.
-
fenixxx
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Fev 28, 2012 21:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Russman » Seg Ago 13, 2012 15:38
por Russman » Seg Ago 13, 2012 15:38
Por indução eu não sei...mas se te ajuda a Lei dessa sequência é:
![A(k)=\frac{1}{2}\left [ (1+\sqrt{2})^k + (1-\sqrt{2})^k \right ]=\sum_{j=0}^{k}\binom{k}{2m}2^m A(k)=\frac{1}{2}\left [ (1+\sqrt{2})^k + (1-\sqrt{2})^k \right ]=\sum_{j=0}^{k}\binom{k}{2m}2^m](/latexrender/pictures/c785973cd9d8ff037928aa047a3e4376.png)
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por fenixxx » Seg Ago 13, 2012 15:43
por fenixxx » Seg Ago 13, 2012 15:43
Tem que ser por indução forte.
-
fenixxx
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Fev 28, 2012 21:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- EXERCITO BRASILEIRO: BRAÇO FORTE, MÃO AMIGA.
por zenildo » Ter Set 17, 2013 17:40
- 0 Respostas
- 1186 Exibições
- Última mensagem por zenildo

Ter Set 17, 2013 17:40
Polinômios
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2680 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- indução
por gramata » Qua Set 02, 2009 16:55
- 0 Respostas
- 1233 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:55
Seminário de Resolução de Problemas
-
- Indução Matemática
por gramata » Qua Set 02, 2009 16:52
- 0 Respostas
- 3063 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:52
Problemas do Cotidiano
-
- Uma prova por indução
por alexandre32100 » Ter Ago 17, 2010 01:11
- 2 Respostas
- 3258 Exibições
- Última mensagem por Guill

Qui Mai 03, 2012 00:01
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
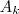 =
= 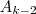 +
+ para todos inteiros k >=3
para todos inteiros k >=3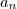 é ?mpar para todo n natural.
é ?mpar para todo n natural.
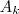 =
= 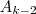 +
+ para todos inteiros k >=3
para todos inteiros k >=3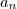 é ?mpar para todo n natural.
é ?mpar para todo n natural.
![A(k)=\frac{1}{2}\left [ (1+\sqrt{2})^k + (1-\sqrt{2})^k \right ]=\sum_{j=0}^{k}\binom{k}{2m}2^m A(k)=\frac{1}{2}\left [ (1+\sqrt{2})^k + (1-\sqrt{2})^k \right ]=\sum_{j=0}^{k}\binom{k}{2m}2^m](/latexrender/pictures/c785973cd9d8ff037928aa047a3e4376.png) .
.

