![\sqrt[]{5+\sqrt[]{24}} \sqrt[]{5+\sqrt[]{24}}](/latexrender/pictures/743f9a80b68560476e80d218e1e6adff.png)
E outra desse tipo:
![\sqrt[]{4.\sqrt[]{6}} \sqrt[]{4.\sqrt[]{6}}](/latexrender/pictures/c8913f0d9893eabbaf3e2da6c1bcf0c9.png)

![\sqrt[]{5+\sqrt[]{24}} \sqrt[]{5+\sqrt[]{24}}](/latexrender/pictures/743f9a80b68560476e80d218e1e6adff.png)
![\sqrt[]{4.\sqrt[]{6}} \sqrt[]{4.\sqrt[]{6}}](/latexrender/pictures/c8913f0d9893eabbaf3e2da6c1bcf0c9.png)

LuizCarlos escreveu:Olá amigo professores, como resolvo uma conta desse tipo!
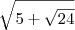 [/quote]
[/quote]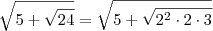
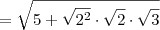
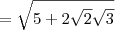
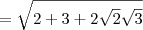


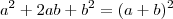 , temos que:
, temos que: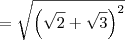
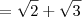
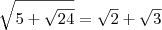
LuizCarlos escreveu:E outra desse tipo:
![\sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6} \sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6}](/latexrender/pictures/41fd9b4b73a19ba898a66f853892ecf9.png)

LuizAquino escreveu:LuizCarlos escreveu:Olá amigo professores, como resolvo uma conta desse tipo!
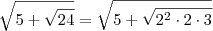
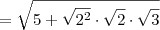
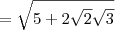
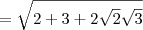


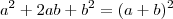 , temos que:
, temos que: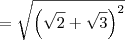
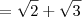
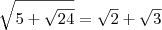
LuizCarlos escreveu:E outra desse tipo:
![\sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6} \sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6}](/latexrender/pictures/41fd9b4b73a19ba898a66f853892ecf9.png) [/quote]
[/quote]
LuizCarlos escreveu:(...) a única maneira de resolver esses tipos de contas, é da forma como você me ensinou, ou existe outro maneira, pois vejo pessoas resolvendo através de uma fórmula, aquela fórmula de radicais duplos, que por sinal, estava olhando, e não consegui entender direito!

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



