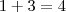por karen » Sáb Mai 05, 2012 15:53
por karen » Sáb Mai 05, 2012 15:53
![1+\sqrt[2]{x+2}=\sqrt[2]{2x+2} 1+\sqrt[2]{x+2}=\sqrt[2]{2x+2}](/latexrender/pictures/61bd8161b9b6bdf1815e583a73ee25ba.png)
Eu resolvi da seguinte forma:
1) Elevei tudo ao quadrado para eliminar a raiz
1+x+2=2x+2
x=1
Na resposta do meu livro está x=7
O que eu fiz de errado?
-
karen
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Mai 03, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
 por DanielFerreira » Sáb Mai 05, 2012 20:42
por DanielFerreira » Sáb Mai 05, 2012 20:42
karen escreveu:![1+\sqrt[2]{x+2}=\sqrt[2]{2x+2} 1+\sqrt[2]{x+2}=\sqrt[2]{2x+2}](/latexrender/pictures/61bd8161b9b6bdf1815e583a73ee25ba.png)
Eu resolvi da seguinte forma:
1) Elevei tudo ao quadrado para eliminar a raiz
1+x+2=2x+2
x=1
Na resposta do meu livro está x=7
O que eu fiz de errado?
Karen,
lembre-se que: (a + b)² = a² +
2.a.b + b²
![1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2} 1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2}](/latexrender/pictures/8689a83f25b9039f63c9432f598acaa6.png)
![(1 + \sqrt[]{x + 2})^2 = (\sqrt[]{2x + 2})^2 (1 + \sqrt[]{x + 2})^2 = (\sqrt[]{2x + 2})^2](/latexrender/pictures/fb4b5d36a03756211e4400ee22dd0d9f.png)
![1 + 2\sqrt[]{x + 2} + x + 2 = 2x + 2 1 + 2\sqrt[]{x + 2} + x + 2 = 2x + 2](/latexrender/pictures/d9b08cc51f5d348714016f514d0d3d23.png)
![2\sqrt[]{x + 2} = x - 1 2\sqrt[]{x + 2} = x - 1](/latexrender/pictures/884acfb35ff432082e978f33930bfa8a.png)
![(2\sqrt[]{x + 2})^2 = (x - 1)^2 (2\sqrt[]{x + 2})^2 = (x - 1)^2](/latexrender/pictures/85369d5a19c347d25de52516d32edef2.png)
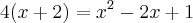
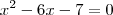
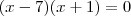
VERIFICANDO QUANDO x = - 1:
![1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2} 1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2}](/latexrender/pictures/8689a83f25b9039f63c9432f598acaa6.png)
![1 + \sqrt[]{- 1 + 2} = \sqrt[]{- 2 + 2} 1 + \sqrt[]{- 1 + 2} = \sqrt[]{- 2 + 2}](/latexrender/pictures/f2d2e06272ed516f0fdbeec40972f7c6.png)
![1 + \sqrt[]{1} = \sqrt[]{0} 1 + \sqrt[]{1} = \sqrt[]{0}](/latexrender/pictures/5a83dbff8e31b11a328d732fea5ccd6c.png)

Falsa!!
VERIFICANDO QUANDO x = 7:
![1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2} 1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2}](/latexrender/pictures/8689a83f25b9039f63c9432f598acaa6.png)
![1 + \sqrt[]{7 + 2} = \sqrt[]{14 + 2} 1 + \sqrt[]{7 + 2} = \sqrt[]{14 + 2}](/latexrender/pictures/9872cff725d372183b532d512d879e59.png)
![1 + \sqrt[]{9} = \sqrt[]{16} 1 + \sqrt[]{9} = \sqrt[]{16}](/latexrender/pictures/1ccb09150ee58c4b82b9a3cc680a81f8.png)
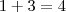
Verdadeira!!
Portanto,
x = 7"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do 1º Grau - Como montar a equação
por macedo1967 » Sáb Out 07, 2017 12:53
- 1 Respostas
- 8037 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:17
Equações
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 3417 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- Equação do 1 Grau
por luanxd » Ter Jan 26, 2010 00:06
- 3 Respostas
- 5523 Exibições
- Última mensagem por Cleyson007

Qua Jan 27, 2010 20:40
Polinômios
-
- equação do 2º grau
por juniorthai » Seg Fev 08, 2010 12:05
- 2 Respostas
- 11755 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 06, 2010 20:48
Trigonometria
-
- equação do 2º grau
por juniorthai » Qui Fev 11, 2010 08:15
- 6 Respostas
- 8357 Exibições
- Última mensagem por lulopes

Sex Dez 08, 2017 20:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![1+\sqrt[2]{x+2}=\sqrt[2]{2x+2} 1+\sqrt[2]{x+2}=\sqrt[2]{2x+2}](/latexrender/pictures/61bd8161b9b6bdf1815e583a73ee25ba.png)

![1+\sqrt[2]{x+2}=\sqrt[2]{2x+2} 1+\sqrt[2]{x+2}=\sqrt[2]{2x+2}](/latexrender/pictures/61bd8161b9b6bdf1815e583a73ee25ba.png)

![1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2} 1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2}](/latexrender/pictures/8689a83f25b9039f63c9432f598acaa6.png)
![(1 + \sqrt[]{x + 2})^2 = (\sqrt[]{2x + 2})^2 (1 + \sqrt[]{x + 2})^2 = (\sqrt[]{2x + 2})^2](/latexrender/pictures/fb4b5d36a03756211e4400ee22dd0d9f.png)
![1 + 2\sqrt[]{x + 2} + x + 2 = 2x + 2 1 + 2\sqrt[]{x + 2} + x + 2 = 2x + 2](/latexrender/pictures/d9b08cc51f5d348714016f514d0d3d23.png)
![2\sqrt[]{x + 2} = x - 1 2\sqrt[]{x + 2} = x - 1](/latexrender/pictures/884acfb35ff432082e978f33930bfa8a.png)
![(2\sqrt[]{x + 2})^2 = (x - 1)^2 (2\sqrt[]{x + 2})^2 = (x - 1)^2](/latexrender/pictures/85369d5a19c347d25de52516d32edef2.png)
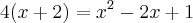
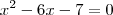
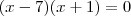
![1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2} 1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2}](/latexrender/pictures/8689a83f25b9039f63c9432f598acaa6.png)
![1 + \sqrt[]{- 1 + 2} = \sqrt[]{- 2 + 2} 1 + \sqrt[]{- 1 + 2} = \sqrt[]{- 2 + 2}](/latexrender/pictures/f2d2e06272ed516f0fdbeec40972f7c6.png)
![1 + \sqrt[]{1} = \sqrt[]{0} 1 + \sqrt[]{1} = \sqrt[]{0}](/latexrender/pictures/5a83dbff8e31b11a328d732fea5ccd6c.png)

![1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2} 1 + \sqrt[]{x + 2} = \sqrt[]{2x + 2}](/latexrender/pictures/8689a83f25b9039f63c9432f598acaa6.png)
![1 + \sqrt[]{7 + 2} = \sqrt[]{14 + 2} 1 + \sqrt[]{7 + 2} = \sqrt[]{14 + 2}](/latexrender/pictures/9872cff725d372183b532d512d879e59.png)
![1 + \sqrt[]{9} = \sqrt[]{16} 1 + \sqrt[]{9} = \sqrt[]{16}](/latexrender/pictures/1ccb09150ee58c4b82b9a3cc680a81f8.png)