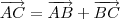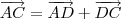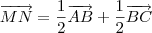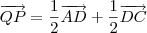Fabio Wanderley escreveu:Meu objetivo é verificar uma conjectura que meu professor de GA passou. É mais ou menos isso: "Dado um quadrilátero qualquer, tomam-se os pontos médios de cada lado. Estes serão os vértices de um paralelogramo."
Eu presumo que o objetivo seja provar essa proposição usando vetores. Eu vou mostrar a ideia e você tenta fazer o exercício.
Considere o quadrilátero ABCD ilustrado na figura abaixo. Tome os pontos médios M, N, P e Q, respectivamente, dos lados AB, BC, CD e DA.
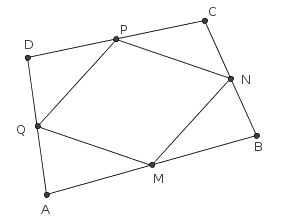
- figura1.png (8.02 KiB) Exibido 1014 vezes
Para provar que o quadrilátero MNPQ é um paralologramo, você precisa provar que o lado MN é paralelo ao lado PQ e o lado NP é paralelo ao lado QM.
Considere a figura abaixo. Observe os vetores

,

,

,

,
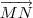
,
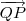
e

.
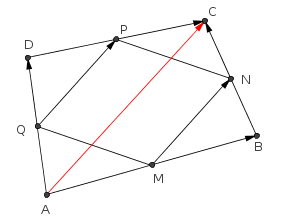
- figura2.png (7.52 KiB) Exibido 1014 vezes
Note as seguintes relações:
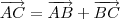
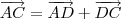
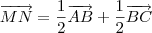
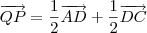
Agora responda: o que você pode concluir dessas relações?




 ,
,  ,
,  ,
,  ,
, 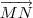 ,
, 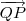 e
e  .
.