de uma ajuda por favor, se a ideia de uma for a mesma para o restante, não ha a
necessidade de fazer d explicar todas, mas me ajudem por favor... =/
1-)
![\frac{\sqrt[]{2 + \sqrt[]{3}}}{\sqrt[]{2 - \sqrt[]{3}}} + \frac{\sqrt[]{2 - \sqrt[]{3}}}{\sqrt[]{2 + \sqrt[]{3}}} \frac{\sqrt[]{2 + \sqrt[]{3}}}{\sqrt[]{2 - \sqrt[]{3}}} + \frac{\sqrt[]{2 - \sqrt[]{3}}}{\sqrt[]{2 + \sqrt[]{3}}}](/latexrender/pictures/35ecde65b10cdaf3c120038af808ba05.png)
Resp: 4
2-)
![\frac{2 + \sqrt[]{3}}{\sqrt[]{2} + \sqrt[]{2 + \sqrt[]{3}}} + \frac{2 - \sqrt[]{3}}{\sqrt[]{2} - \sqrt[]{2 - \sqrt[]{3}}} \frac{2 + \sqrt[]{3}}{\sqrt[]{2} + \sqrt[]{2 + \sqrt[]{3}}} + \frac{2 - \sqrt[]{3}}{\sqrt[]{2} - \sqrt[]{2 - \sqrt[]{3}}}](/latexrender/pictures/9b4c6786a084bd620c64b381db12716f.png)
Resp:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
3-)
![\frac{\sqrt[]{48} + \sqrt[]{27} - \sqrt[]{125}}{\sqrt[]{12} + \sqrt[]{108} - \sqrt[]{180}} \frac{\sqrt[]{48} + \sqrt[]{27} - \sqrt[]{125}}{\sqrt[]{12} + \sqrt[]{108} - \sqrt[]{180}}](/latexrender/pictures/87979b718723c54557ad9f2111fc3fb3.png)
eu consegui o começo, encontrei:
![\frac{7\sqrt[]{3} - 5\sqrt[]{5}}{8\sqrt[]{3} - 6\sqrt[]{5}} \frac{7\sqrt[]{3} - 5\sqrt[]{5}}{8\sqrt[]{3} - 6\sqrt[]{5}}](/latexrender/pictures/d3e33ec92e254a04e0ea3c8198ea9382.png)
e não sei resolver =/
Resp:
![\frac{9+ \sqrt[]{15}}{6} \frac{9+ \sqrt[]{15}}{6}](/latexrender/pictures/b1b215d3c0c065ef85b103a5b4d74b17.png)
4-)
![\frac{\sqrt[]{3 - 2 \sqrt[]{2}}}{\sqrt[]{17 - 12 \sqrt[]{2}}} - \frac{\sqrt[]{3 + 2 \sqrt[]{2}}}{\sqrt[]{17 + 12 \sqrt[]{2}}} \frac{\sqrt[]{3 - 2 \sqrt[]{2}}}{\sqrt[]{17 - 12 \sqrt[]{2}}} - \frac{\sqrt[]{3 + 2 \sqrt[]{2}}}{\sqrt[]{17 + 12 \sqrt[]{2}}}](/latexrender/pictures/76f903f77417434c33957f521e57388c.png)
Resp: 2

![\frac{\sqrt[]{2 + \sqrt[]{3}}}{\sqrt[]{2 - \sqrt[]{3}}} + \frac{\sqrt[]{2 - \sqrt[]{3}}}{\sqrt[]{2 + \sqrt[]{3}}} \frac{\sqrt[]{2 + \sqrt[]{3}}}{\sqrt[]{2 - \sqrt[]{3}}} + \frac{\sqrt[]{2 - \sqrt[]{3}}}{\sqrt[]{2 + \sqrt[]{3}}}](/latexrender/pictures/35ecde65b10cdaf3c120038af808ba05.png)
![\frac{2 + \sqrt[]{3}}{\sqrt[]{2} + \sqrt[]{2 + \sqrt[]{3}}} + \frac{2 - \sqrt[]{3}}{\sqrt[]{2} - \sqrt[]{2 - \sqrt[]{3}}} \frac{2 + \sqrt[]{3}}{\sqrt[]{2} + \sqrt[]{2 + \sqrt[]{3}}} + \frac{2 - \sqrt[]{3}}{\sqrt[]{2} - \sqrt[]{2 - \sqrt[]{3}}}](/latexrender/pictures/9b4c6786a084bd620c64b381db12716f.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
![\frac{\sqrt[]{48} + \sqrt[]{27} - \sqrt[]{125}}{\sqrt[]{12} + \sqrt[]{108} - \sqrt[]{180}} \frac{\sqrt[]{48} + \sqrt[]{27} - \sqrt[]{125}}{\sqrt[]{12} + \sqrt[]{108} - \sqrt[]{180}}](/latexrender/pictures/87979b718723c54557ad9f2111fc3fb3.png)
![\frac{7\sqrt[]{3} - 5\sqrt[]{5}}{8\sqrt[]{3} - 6\sqrt[]{5}} \frac{7\sqrt[]{3} - 5\sqrt[]{5}}{8\sqrt[]{3} - 6\sqrt[]{5}}](/latexrender/pictures/d3e33ec92e254a04e0ea3c8198ea9382.png)
![\frac{9+ \sqrt[]{15}}{6} \frac{9+ \sqrt[]{15}}{6}](/latexrender/pictures/b1b215d3c0c065ef85b103a5b4d74b17.png)
![\frac{\sqrt[]{3 - 2 \sqrt[]{2}}}{\sqrt[]{17 - 12 \sqrt[]{2}}} - \frac{\sqrt[]{3 + 2 \sqrt[]{2}}}{\sqrt[]{17 + 12 \sqrt[]{2}}} \frac{\sqrt[]{3 - 2 \sqrt[]{2}}}{\sqrt[]{17 - 12 \sqrt[]{2}}} - \frac{\sqrt[]{3 + 2 \sqrt[]{2}}}{\sqrt[]{17 + 12 \sqrt[]{2}}}](/latexrender/pictures/76f903f77417434c33957f521e57388c.png)

nathyn escreveu:1-)
Resp: 4
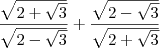
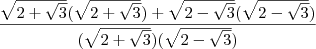
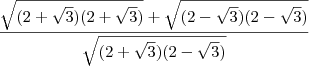
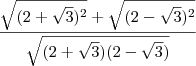
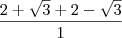

nathyn escreveu:3-)
eu consegui o começo, encontrei:
e não sei resolver =/
Resp:
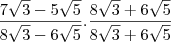
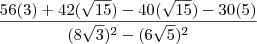
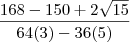
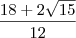
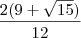
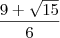


![\frac{\sqrt[]{3 - 2 \sqrt[]{2}}}{\sqrt[]{17 - 12 \sqrt[]{2}}} - \frac{\sqrt[]{3 + 2 \sqrt[]{2}}}{\sqrt[]{17 + 12 \sqrt[]{2}}} \frac{\sqrt[]{3 - 2 \sqrt[]{2}}}{\sqrt[]{17 - 12 \sqrt[]{2}}} - \frac{\sqrt[]{3 + 2 \sqrt[]{2}}}{\sqrt[]{17 + 12 \sqrt[]{2}}}](/latexrender/pictures/76f903f77417434c33957f521e57388c.png)
![\frac{\left(\sqrt[]{3-2\sqrt[]{2}} \right)\left(\sqrt[]{17 + 12\sqrt[]{2}} \right) - \left(\sqrt[]{3 + 2\sqrt[]{2}} \right)\left(\sqrt[]{17 - 12\sqrt[]{2}} \right)}{\left(\sqrt[]{17 + 12\sqrt[]{2}} \right)\left(\sqrt[]{17 - 12\sqrt[]{2}} \right)} \frac{\left(\sqrt[]{3-2\sqrt[]{2}} \right)\left(\sqrt[]{17 + 12\sqrt[]{2}} \right) - \left(\sqrt[]{3 + 2\sqrt[]{2}} \right)\left(\sqrt[]{17 - 12\sqrt[]{2}} \right)}{\left(\sqrt[]{17 + 12\sqrt[]{2}} \right)\left(\sqrt[]{17 - 12\sqrt[]{2}} \right)}](/latexrender/pictures/85d62d908af9a950d7bfeb1b72e8adec.png)
![\frac{= \sqrt[]{51 + 36\sqrt[]{2} - 34\sqrt[]{2} - 48} - \sqrt[]{51 - 36\sqrt[]{2} + 34\sqrt[]{2} - 48}}{\sqrt[]{1}} \frac{= \sqrt[]{51 + 36\sqrt[]{2} - 34\sqrt[]{2} - 48} - \sqrt[]{51 - 36\sqrt[]{2} + 34\sqrt[]{2} - 48}}{\sqrt[]{1}}](/latexrender/pictures/688ecbb575c15b1deb2f3f6835102f04.png)
![\sqrt[]{3+ 2\sqrt[]{2}} - \sqrt[]{3 - 2\sqrt[]{2}} \sqrt[]{3+ 2\sqrt[]{2}} - \sqrt[]{3 - 2\sqrt[]{2}}](/latexrender/pictures/0c01fffafc2d6ea8cd11665d5a293ed7.png)


nathyn escreveu:Eu entendi a ideia, mas a segunda não consegui fazer pq a ideia é diferente =/,
a ultima eu fiz mas nao sei onde estou errando...
nathyn escreveu:
e agora nao sei como continuo, isso se estiver certo =/

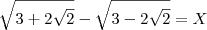
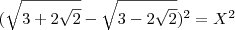


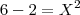



![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) e não 2 =(.
e não 2 =(.
nathyn escreveu:aah nao, ta errado pq resposta ée não 2 =(.
Mas brigada ae pela ajuda =)



![\frac{2 + \sqrt[]{3}}{\sqrt[]{2} + \sqrt[]{2 + \sqrt[]{3}}} + \frac{2 - \sqrt[]{3}}{\sqrt[]{2} - \sqrt[]{2 - \sqrt[]{3}}} \frac{2 + \sqrt[]{3}}{\sqrt[]{2} + \sqrt[]{2 + \sqrt[]{3}}} + \frac{2 - \sqrt[]{3}}{\sqrt[]{2} - \sqrt[]{2 - \sqrt[]{3}}}](/latexrender/pictures/9b4c6786a084bd620c64b381db12716f.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
![\frac{\left(2 + \sqrt[]{3} \right)\left(\sqrt[]{2} - \sqrt[]{2 + \sqrt[]{3}} \right)}{2 - 2 -\sqrt[]{3}} + \frac{\left(2 - \sqrt[]{3} \right)\left(\sqrt[]{2} + \sqrt[]{2 - \sqrt[]{3}} \right)}{2 - 2 +\sqrt[]{3}} \frac{\left(2 + \sqrt[]{3} \right)\left(\sqrt[]{2} - \sqrt[]{2 + \sqrt[]{3}} \right)}{2 - 2 -\sqrt[]{3}} + \frac{\left(2 - \sqrt[]{3} \right)\left(\sqrt[]{2} + \sqrt[]{2 - \sqrt[]{3}} \right)}{2 - 2 +\sqrt[]{3}}](/latexrender/pictures/c156b2440bf122cb7cbc7eeafcbe3205.png)
![- \sqrt[]{3} - \sqrt[]{3}](/latexrender/pictures/5146764d594e41cc1e0df3c201b01a02.png) , o sinal do numerador da primeira foram mudados, ficando:
, o sinal do numerador da primeira foram mudados, ficando:![\frac{-2 \sqrt[]{2} + 2\sqrt[]{2 + \sqrt[]{3}} -\sqrt[]{6} + \sqrt[]{6 + 3\sqrt[]{3}}}{\sqrt[]{3}} + \frac{2 \sqrt[]{2} + 2\sqrt[]{2 - \sqrt[]{3}} -\sqrt[]{6} - \sqrt[]{6 - 3\sqrt[]{3}}}{\sqrt[]{3}} \frac{-2 \sqrt[]{2} + 2\sqrt[]{2 + \sqrt[]{3}} -\sqrt[]{6} + \sqrt[]{6 + 3\sqrt[]{3}}}{\sqrt[]{3}} + \frac{2 \sqrt[]{2} + 2\sqrt[]{2 - \sqrt[]{3}} -\sqrt[]{6} - \sqrt[]{6 - 3\sqrt[]{3}}}{\sqrt[]{3}}](/latexrender/pictures/b4435ab6b21a3b089fcf9ce7455b9d0a.png)
![\frac{2\sqrt[]{2 + \sqrt[]{3}} - 2\sqrt[]{6} + \sqrt[]{6 + 3\sqrt[]{3}} - \sqrt[]{6 - 3\sqrt[]{3}}}{\sqrt[]{3}} \frac{2\sqrt[]{2 + \sqrt[]{3}} - 2\sqrt[]{6} + \sqrt[]{6 + 3\sqrt[]{3}} - \sqrt[]{6 - 3\sqrt[]{3}}}{\sqrt[]{3}}](/latexrender/pictures/064eac5f877c0f5c68ae7391c1b032a1.png)
![\frac{2\sqrt[]{6 + 3\sqrt[]{3}} -6\sqrt[]{2} + \sqrt[]{18 + 9\sqrt[]{3}} - \sqrt[]{18 - 9\sqrt[]{3}}}{3} \frac{2\sqrt[]{6 + 3\sqrt[]{3}} -6\sqrt[]{2} + \sqrt[]{18 + 9\sqrt[]{3}} - \sqrt[]{18 - 9\sqrt[]{3}}}{3}](/latexrender/pictures/57d4664c62c4af3e7dd33bd2a9571f49.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



