 por clabonfim » Seg Jan 16, 2012 01:22
por clabonfim » Seg Jan 16, 2012 01:22
Diz-se que um número inteiro positivo x é um número perfeito, quando é a soma de todos
os seus divisores positivos, exceto ele próprio. Por exemplo, 28 é um número perfeito, pois
28 = 1 + 2 + 4 + 7 + 14. A última proposição do nono livro dos Elementos de Euclides prova
que se n é um inteiro positivo, tal que 2^n ?1 é um número primo, então 2^(n–1)(2^n ?1) é um número
perfeito. Euler provou que todo número perfeito par tem essa forma, mas ainda não são
conhecidos números perfeitos ímpares.
O menor elemento do conjunto P = {n ? / 2^(n?1)(2^n ?1) > 1128}, para o qual 2n–1(2n?1) é um número
perfeito, é
A) 5 C) 7 E) 9
B) 6 D) 8
-
clabonfim
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Ago 08, 2011 04:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Seg Jan 16, 2012 21:37
por fraol » Seg Jan 16, 2012 21:37
Não entendi, ao certo, as expressões contidas no trecho:
O menor elemento do conjunto P = {n ? / 2^(n?1)(2^n ?1) > 1128}, para o qual 2n–1(2n?1) é um número
perfeito, é
Você tem como melhorar o texto usando Latex, quem sabe usando o Editor de Fórmulas?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por fraol » Seg Jan 16, 2012 22:59
por fraol » Seg Jan 16, 2012 22:59
Revendo um pouco o assunto números perfeitos, acredito que a expressão seja:
O menor elemento do conjunto
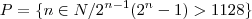
, para o qual
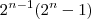
é um número perfeito, é
Se assim o for, usando a informação dada: "se
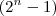
é um número primo, então
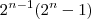
é um número perfeito" e o fato de que "se
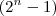
é um número primo, então

também é primo", concluí-se que
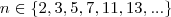
.
Daqui em diante, ou tentamos isolar o

na expressão
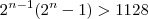
via algum recurso algébrico ( tentei mas não cheguei a bom termo ), ou testamos alguns números primos posto que 1128 é um número relativamente pequeno e não será difícil encontrar o tal n.
Outra alternativa, que não é o caso em um teste ou prova, mas pode ser usado em caso de pesquisa é recorrer a uma tabela de números perfeitos conhecidos, ou mesmo aplicar a fórmula em uma planilha de cálculo.
Se algum outro colega tiver alguma outra forma, manda pra cá.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Arkanus Darondra » Seg Jan 16, 2012 23:08
por Arkanus Darondra » Seg Jan 16, 2012 23:08
fraol escreveu:Se algum outro colega tiver alguma outra forma, manda pra cá.
Boa Noite.
Ele postou a mesma questão aqui e no fórum pir2.
Ela já foi respondida e a resposta é
n = 7
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Seg Jan 16, 2012 23:31
por fraol » Seg Jan 16, 2012 23:31
Obrigado Arkanus!
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7723 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13230 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13022 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6092 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8708 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



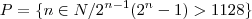 , para o qual
, para o qual 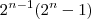 é um número perfeito, é
é um número perfeito, é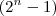 é um número primo, então
é um número primo, então  também é primo", concluí-se que
também é primo", concluí-se que 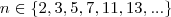 .
.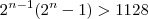 via algum recurso algébrico ( tentei mas não cheguei a bom termo ), ou testamos alguns números primos posto que 1128 é um número relativamente pequeno e não será difícil encontrar o tal n.
via algum recurso algébrico ( tentei mas não cheguei a bom termo ), ou testamos alguns números primos posto que 1128 é um número relativamente pequeno e não será difícil encontrar o tal n.