Estou tendo dificuldades de resolver está inequação, se tiver alguém que puder me ajudar, agradeço....
2. Representemos por max(a, b) o maior dos números a e b. Resolva as inequações para
(3x^2+10x+8)/(x+2) < 2x +5







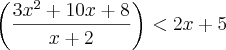
 . Entao o polinômio é divisível por
. Entao o polinômio é divisível por  , em outras palavras, o quociente
, em outras palavras, o quociente 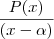 é inteiro (não tem resto)
é inteiro (não tem resto) 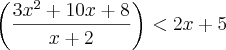
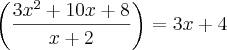
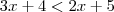





Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.



