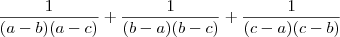 é:
é:a) a + b + c
b) sempre zero
c) a.b.c
d) 3(a + b + c)
e)
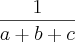

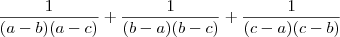 é:
é: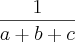




Abelardo escreveu:vc considerou que (a - b) é igual a (b - a)? não consegui simplificá-lo..

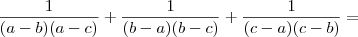
![= \frac{1}{(a-b)(a-c)} + \frac{1}{[(-1)(a-b)][(-1)(c-b)]} +\frac{1}{[(-1)(a-c)](c-b)} = \frac{1}{(a-b)(a-c)} + \frac{1}{[(-1)(a-b)][(-1)(c-b)]} +\frac{1}{[(-1)(a-c)](c-b)}](/latexrender/pictures/058cca2cdd8c50d9460e7d0d0ea8b176.png)




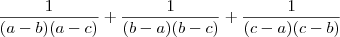 (encontrei zero)
(encontrei zero)  (encontrei - 1)
(encontrei - 1)





Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: