Não podemos "multiplicar em cruz" nas inequações da mesma forma que podemos nas equações.
Vejamos um exemplo.
Exercício: Determine a solução da inequação

sendo x um número real.
Solução Errada


Se essa é a solução correta, então para x=1 a inequação deveria ser válida, correto? E o que acontece se você substituir x por 1 na inequação? Surpresa! Você teria que 0 > 5/2!
Solução Correta


Sabemos que a função f(x)=-3x+8 é positiva para x < 8/3 e negativa para x > 8/3. Por outro lado, a função g(x)=2x-4 é positiva para x>2 e negativa para x<2. Fazendo a análise dos sinais das funções, a solução da inequação é 2<x<8/3.
E agora, você deve estar se perguntando: por que será que não posso "multiplicar em cruz" nas inequações?
A resposta está na seguinte propriedade de inequações:
Se a>b, então:
(i) ac > bc, se c > 0
(ii) ac < bc, se c < 0
No exercício acima, quando nós fizemos (de maneira errada)
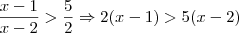
, podemos enxergar que realizamos duas operações:
(a) Multiplicamos toda a inequação por 2, que como é um número positivo não altera a inequação (propriedade (i)).
Isto é, nós fizemos:
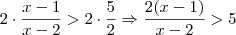
(b) Em seguida, multiplicamos toda a inequação por (x-2). Aqui é que mora o problema! O número (x-2) pode ser negativo ou pode ser positivo!
Quando (x-2) for positivo (portanto x>2), a inequação não se altera e teríamos que

(Propriedade (i))
Mas, quando (x-2) for negativo (portanto x<2), o correto seria ficarmos com

(Propriedade (ii))
Note que essa última solução não faz sentido, já que com x<2 nós obtemos que a inequação é tal que
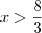
.
Já a primeira solução está correta: para x>2 vai ocorrer que a inequação é tal que

. Portanto o número x procurado é tal que
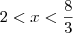
.







 sendo x um número real.
sendo x um número real.

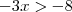




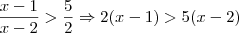 , podemos enxergar que realizamos duas operações:
, podemos enxergar que realizamos duas operações: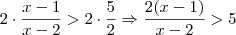
 (Propriedade (i))
(Propriedade (i)) (Propriedade (ii))
(Propriedade (ii))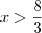 .
. . Portanto o número x procurado é tal que
. Portanto o número x procurado é tal que 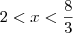 .
.


, então
. A minha pergunta é a seguinte porque eu não posso aplicar esta propriedade nesta questão?
 ?
?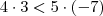 . Mas, isso é falso!
. Mas, isso é falso!

 .
.
 :
: