 por lucas7 » Qui Fev 17, 2011 20:55
por lucas7 » Qui Fev 17, 2011 20:55
Boa Noite! Preciso de ajuda:
17)
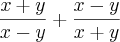
como que eu igualo esses denominadores? Eu não entendi como faz o mmc.
Outro exemplo:
19)

Preciso de uma solução numa maneira bem explicativa, passo a passo, para eu poder entender.
Obrigado.
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por Cleyson007 » Qui Fev 17, 2011 21:27
por Cleyson007 » Qui Fev 17, 2011 21:27
Boa noite Lucas!
17)
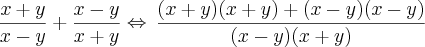
O procedimento é simples: O m.m.c é (x+y)(x-y) (Resolve dividindo o mmc pelo denominador, o resultado deverá ser multiplicado pelo numerador).
19) Repare que (1 - 3x) (1 + 3x) = (1 - 9x²) --> Logo o m.m.c é (1 - 9x²).
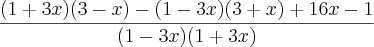
(Aqui o procedimento adotado é o mesmo do exercício 17)
Agora tente desenvolver os parênteses sozinho, ok? Surgindo dúvidas comunique.
Abraços.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Qui Fev 17, 2011 21:30
por Cleyson007 » Qui Fev 17, 2011 21:30
Boa noite Lucas!
17)
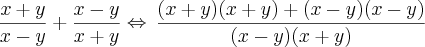
O procedimento é simples: O m.m.c é (x+y)(x-y) (Resolve dividindo o mmc pelo denominador, o resultado deverá ser multiplicado pelo numerador).
Resolvendo os parênteses do numerador:

19) Repare que (1 - 3x) (1 + 3x) = (1 - 9x²) --> Logo o m.m.c é (1 - 9x²).
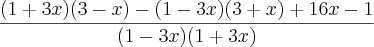
(Aqui o procedimento adotado é o mesmo do exercício 17)
Agora tente desenvolver os parênteses sozinho, ok? Surgindo dúvidas comunique.
Abraços.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por lucas7 » Qui Fev 17, 2011 21:42
por lucas7 » Qui Fev 17, 2011 21:42
Tentei, mas acho que não deu certo:
17)

=
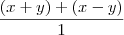
=

.... Segundo o gabarito seria

Eu cortei as multiplicações para simplificar, e depois somei onde tinha o sinal de mais, qual o erro?!
ps: cheguei ao resultado certo da 17, sem simplificar ela. por que não dá pra cortar?
19)
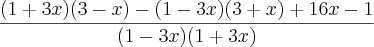
=

=
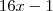
outra tentativa, sem simplificar inicialmente:
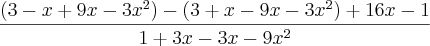
=
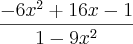
ps: consegui, o sinal negativo antes dos parentes altera a positividade de todos os números dentro do parênteses.
Segundo o gabarito:
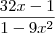
Obrigado
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por lucas7 » Sex Fev 18, 2011 00:12
por lucas7 » Sex Fev 18, 2011 00:12
Outra:
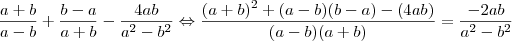
O gabarito diz que a resposta é 0. Qual o erro?
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por Cleyson007 » Sex Fev 18, 2011 18:23
por Cleyson007 » Sex Fev 18, 2011 18:23
Boa tarde Lucas!
Respondendo seu último exercício postado:

Vou resolver passo-a-passo para você entender melhor o que acontece. Veja:

Desenvolvendo o numerador e o denominador, temos:

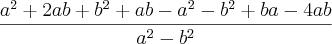
Somando os termos do numerador perceberá que dará 0, logo:
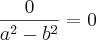
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Frações Algébricas] Como simplifico essa fração?
 por Kah » Qua Mar 18, 2015 17:44
por Kah » Qua Mar 18, 2015 17:44
- 1 Respostas
- 2153 Exibições
- Última mensagem por Russman

Qua Mar 18, 2015 22:38
Álgebra Elementar
-
- frações algebricas
por tamirosa » Qui Out 29, 2009 20:11
- 1 Respostas
- 3307 Exibições
- Última mensagem por Molina

Sex Out 30, 2009 11:37
Álgebra Elementar
-
- Frações Algébricas
por LuizCarlos » Dom Ago 07, 2011 21:45
- 5 Respostas
- 2927 Exibições
- Última mensagem por MarceloFantini

Seg Ago 08, 2011 02:06
Álgebra Elementar
-
- Frações Algébricas
por LuizCarlos » Qui Abr 19, 2012 14:33
- 4 Respostas
- 2188 Exibições
- Última mensagem por LuizCarlos

Qui Abr 19, 2012 17:59
Álgebra Elementar
-
- Frações Algébricas Ajudem-me!
por Jansen » Seg Ago 31, 2009 23:32
- 0 Respostas
- 1671 Exibições
- Última mensagem por Jansen

Seg Ago 31, 2009 23:32
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
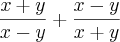 como que eu igualo esses denominadores? Eu não entendi como faz o mmc.
como que eu igualo esses denominadores? Eu não entendi como faz o mmc.

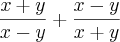 como que eu igualo esses denominadores? Eu não entendi como faz o mmc.
como que eu igualo esses denominadores? Eu não entendi como faz o mmc.

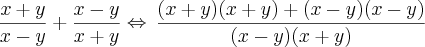
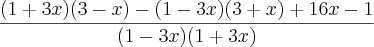 (Aqui o procedimento adotado é o mesmo do exercício 17)
(Aqui o procedimento adotado é o mesmo do exercício 17)
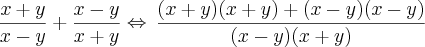

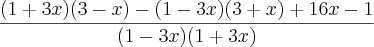 (Aqui o procedimento adotado é o mesmo do exercício 17)
(Aqui o procedimento adotado é o mesmo do exercício 17)
 =
= 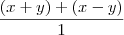 =
=  .... Segundo o gabarito seria
.... Segundo o gabarito seria 
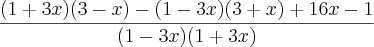 =
=  =
= 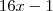
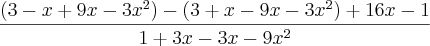 =
= 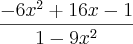
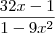

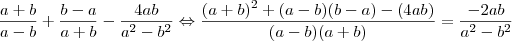




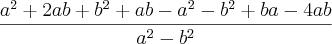
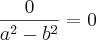




 , avisa que eu resolvo.
, avisa que eu resolvo.

