por c_zaidan » Qua Dez 08, 2010 17:51
SOCORRO!3 profissionais fazem 24 peças em 2 horas, e 4 aprendizes fazem 16 peças em 3 horas. Em quantas horas 2 profissionais e 3 aprendizes farão 48 peças?
Não tenho ideia de como fazer qdo tenho prof e aprendizes juntos. Sei q a razão entre as pessoas e as peças é direta e q entre as pessoas e o tempo é inversa. Só
Alguém podia me ajudar?
-
c_zaidan
- Novo Usuário
-
- Mensagens: 5
- Registrado em: Sex Out 22, 2010 15:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
por PedroSantos » Qua Dez 08, 2010 18:58
Primeiro define 3 variaveis.Para a quantidade de peças produzidas por hora pelos profissionais, a variável
p.Para a quantidade de peças produzidas por hora pelos aprendizes a variável
a e por fim para a quantidade de horas a variável
h.
Escrevemos três equações:
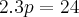
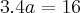
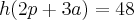
Agora é resolver o sistema de 3 equações.
-
PedroSantos
- Usuário Ativo
-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
por c_zaidan » Qua Dez 08, 2010 19:46
Mas nn tem nada a ver com regra de 3 nn? Não teria que mostrar que a relação tempo/qtde de pessoas é inversa?
Se for um sistema, to boiando no assunto msm! Vou tentar resolver o sistema aqui.
Muito obrigada
-
c_zaidan
- Novo Usuário
-
- Mensagens: 5
- Registrado em: Sex Out 22, 2010 15:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- resultado diferente - PG
por jose henrique » Qui Set 30, 2010 23:50
- 4 Respostas
- 3199 Exibições
- Última mensagem por MarceloFantini
Ter Out 05, 2010 01:18
Progressões
-
- [Limite]de sen(x)/x = 1 só se x diferente de ...
por marcosmuscul » Qui Mar 28, 2013 20:34
- 3 Respostas
- 2845 Exibições
- Última mensagem por marcosmuscul
Sex Mar 29, 2013 14:00
Cálculo: Limites, Derivadas e Integrais
-
- gabarito diferente da resposta
por jose henrique » Ter Out 12, 2010 01:10
- 2 Respostas
- 2121 Exibições
- Última mensagem por jose henrique
Seg Out 25, 2010 21:45
Funções
-
- resultado diferente da resposta
por natanskt » Seg Dez 06, 2010 13:39
- 1 Respostas
- 2184 Exibições
- Última mensagem por Elcioschin
Seg Dez 06, 2010 14:01
Binômio de Newton
-
- P.A. com razão diferente a partir do A2
por livio isbrecht » Sex Jan 06, 2012 21:44
- 6 Respostas
- 8117 Exibições
- Última mensagem por DanielFerreira
Dom Jan 08, 2012 17:49
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
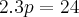
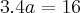
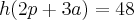
