O autor do meu livro de estudos matemáticos (Ibirajara Favilli), afirma que a seguinte sentença:
 NÃO ESTÁ CONTIDO EM {1,2,{
NÃO ESTÁ CONTIDO EM {1,2,{ }}
}}é uma sentença VERADEIRA.
Minhs dúvida é:
1) Como essa sentença, supostamente , foi considerada verdadeira pelo autor? Se outrora, este próprio autor afirma que:
 é subconjunto de todo e qualquer conjunto.
é subconjunto de todo e qualquer conjunto.Eu estou tentando visualizar, o que eu estou fazendo errado. Mas não estou conseguindo entender.
Por favor, alguém pode me dar uma luz?

Obrigado!
ps: não achei o sinal de "NÃO ESTÁ CONTIDO" no editor de fórmulas.


 relaciona apenas
relaciona apenas 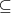 em {1,2{
em {1,2{

 .
.



