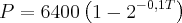 descreve o crescimento de uma população de microorganismos T dias após o instante
descreve o crescimento de uma população de microorganismos T dias após o instantezero. O valor de P é superior a 6300 se, e somente se, T satisfazer a condição
a) 2<t<16
b) t<60
c) t<30
d) t>60
e) 32<t<64
Eu consegui resolver por substituição dos valores das respostas na inequação
mas isso demora muito, alguem consegue resolver essa inequação?



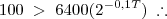
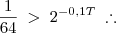
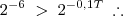
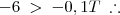
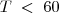

![[-6 \; > \; -0,1T] . (-1) \; \therefore [-6 \; > \; -0,1T] . (-1) \; \therefore](/latexrender/pictures/de896caaf8b3995cd28267e2ccc663e4.png)


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)