 por giancarlo_vanitelli » Ter Nov 25, 2014 15:57
por giancarlo_vanitelli » Ter Nov 25, 2014 15:57
Boa tarde, gostaria de saber o que estou fazendo de errado, nesse exercício.

A resposta do gabarito é:
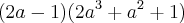
-
giancarlo_vanitelli
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Nov 22, 2014 16:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: cursando
 por DanielFerreira » Sáb Dez 13, 2014 15:25
por DanielFerreira » Sáb Dez 13, 2014 15:25
Giancarlo,
boa tarde!
Não entendi como concluiu a terceira linha!
![\\ 4a^4 - a^2 + 2a - 1 = \\\\ 4a^4 - (a^2 - 2a + 1) = \\\\ (2a^2)^2 - (a - 1)^2 = \\\\ \left [ (2a^2) + (a - 1) \right ] \cdot \left [ (2a^2) - (a - 1) \right ] = \\\\ \boxed{(2a^2 + a - 1)(2a^2 - a + 1)} \\ 4a^4 - a^2 + 2a - 1 = \\\\ 4a^4 - (a^2 - 2a + 1) = \\\\ (2a^2)^2 - (a - 1)^2 = \\\\ \left [ (2a^2) + (a - 1) \right ] \cdot \left [ (2a^2) - (a - 1) \right ] = \\\\ \boxed{(2a^2 + a - 1)(2a^2 - a + 1)}](/latexrender/pictures/c67797a2602ecb17912434a6341c4abb.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fatoração] O que estou fazendo de errado?
por giancarlo_vanitelli » Sáb Nov 22, 2014 19:02
- 3 Respostas
- 1729 Exibições
- Última mensagem por DanielFerreira

Dom Nov 23, 2014 21:47
Álgebra Elementar
-
- [Fatoração] O que estou fazendo de errado?
por giancarlo_vanitelli » Ter Nov 25, 2014 16:22
- 4 Respostas
- 2044 Exibições
- Última mensagem por nakagumahissao

Qua Nov 26, 2014 19:28
Álgebra Elementar
-
- O que estou fazendo errado
por micheli57 » Seg Mar 02, 2015 21:47
- 2 Respostas
- 2192 Exibições
- Última mensagem por micheli57

Ter Mar 03, 2015 09:06
Álgebra Elementar
-
- O que estou fazendo errado
por micheli57 » Seg Mar 02, 2015 21:57
- 1 Respostas
- 1643 Exibições
- Última mensagem por Russman

Seg Mar 02, 2015 22:56
Álgebra Elementar
-
- [INEQUAÇÕES] O que estou fazendo de errado?
por homerbrasil » Qua Jan 11, 2012 16:44
- 5 Respostas
- 2894 Exibições
- Última mensagem por homerbrasil

Qui Jan 12, 2012 16:28
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

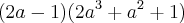


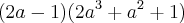

![\\ 4a^4 - a^2 + 2a - 1 = \\\\ 4a^4 - (a^2 - 2a + 1) = \\\\ (2a^2)^2 - (a - 1)^2 = \\\\ \left [ (2a^2) + (a - 1) \right ] \cdot \left [ (2a^2) - (a - 1) \right ] = \\\\ \boxed{(2a^2 + a - 1)(2a^2 - a + 1)} \\ 4a^4 - a^2 + 2a - 1 = \\\\ 4a^4 - (a^2 - 2a + 1) = \\\\ (2a^2)^2 - (a - 1)^2 = \\\\ \left [ (2a^2) + (a - 1) \right ] \cdot \left [ (2a^2) - (a - 1) \right ] = \\\\ \boxed{(2a^2 + a - 1)(2a^2 - a + 1)}](/latexrender/pictures/c67797a2602ecb17912434a6341c4abb.png)

